题目内容

在同一坐标系下函数y=-x+a和y=ax图象可能是（　　）
A、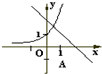
B、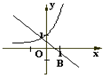
C、
D、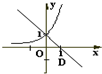
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：分类讨论函数的单调性，在y轴上的交点的位置，可以选答案．
解答： 解：解：函数y=-x+a和y=ax，
当a＞1时，y=-x+a，单调递减，y=ax单调递增，
且直线在y轴交点为在（0，1）上边，
A正确，B．D不正确
当0＜a＜1时，一次函数单调递减，指数函数单调递减，且直线在y轴交点为在（0，1）下边，
C不正确
故选：A
点评：本题考查了函数的图象和性质求解问题，属于容易题．
练习册系列答案
相关题目
若函数g（x）=x2+2x-12m在区间（-∞，-2）与（-2，1）上各有一个实根，则实数m的取值范围是（　　）
A、（-∞，
1
4
）
B、（
1
4
+∞）
C、（0，
1
4
）
D、（
1
4
，1）
画出y=x -
1
2
的函数图象．
给出如下五个结论：
①存在α∈（0，
π
2
）使sinα+cosα=
1
3

②存在区间（a，b）使y=cosx为减函数而sinx＜0
③y=tanx在其定义域内为增函数
④y=cos2x+sin（
π
2
-x）既有最大、最小值，又是偶函数
⑤y=|sin（2x+
π
6
）|最小正周期为π
其中正确结论的序号是
 
．
已知三个实数a，b，c，当c＞0时满足：b≤2a+3c且bc=a2，则
b
a-2c
的取值范围是
 
．
在如图所示的茎叶图中，甲、乙两组数据的中位数分别是
 
、
 
．
已知函数f（x）=
-x+2(x＞1)
x2(-1≤x≤1)
x+2(x＜-1)
．
（1）求f（f（
5
2
））的值；
（2）画出函数的图象，并根据图象写出函数的值域和单调区间；
（3）若函数g（x）=f（x）-m有四个不同零点，求m的取值范围，并求出这四个零点的和．
已知两点A（-2，1），B（1，5），点C是圆x2+y2-2x+4y-4=0上的动点，则△ABC面积的最大值为（　　）
A、35B、18C、16D、8
给出程序框图如图，则输出的结果为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网