题目内容
把矩形ABCD沿对角线BD折起,形成三棱锥C-ABD的正视图和俯视图如图所示,则侧视图的面积为 .


考点:简单空间图形的三视图
专题:空间位置关系与距离
分析:根据几何体的三视图,得出该几何体是底面为直角三角形BAD,且一侧面CBD垂直于底面的三棱锥,画出图形,求出它的侧视图的面积来.
解答:
 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;
该几何体是底面为直角三角形BAD,且一侧面CBD垂直于底面的三棱锥,
如图所示;
∴BD=5,
∴Rt△ABD与Rt△CBD的高相等,
即CE=AF=
=
,
∴侧视图是腰长为
的等腰三角形,
面积为
×
×
=
.
故答案为:
.
 解:根据几何体的三视图,得;
解:根据几何体的三视图,得;该几何体是底面为直角三角形BAD,且一侧面CBD垂直于底面的三棱锥,
如图所示;
∴BD=5,
∴Rt△ABD与Rt△CBD的高相等,
即CE=AF=
| 3×4 |
| 5 |
| 12 |
| 5 |
∴侧视图是腰长为
| 12 |
| 5 |
面积为
| 1 |
| 2 |
| 12 |
| 5 |
| 12 |
| 5 |
| 72 |
| 25 |
故答案为:
| 72 |
| 25 |
点评:本题考查了空间几何体的三视图的应用问题,解题的关键是根据三视图得出该几何体的结构特征是什么.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
 如图,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=
如图,在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=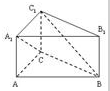 已知直三棱柱ABC--A1B1C1中,AB=4,AC=AA1=2,∠ACB=90°.
已知直三棱柱ABC--A1B1C1中,AB=4,AC=AA1=2,∠ACB=90°.