题目内容
已知向量
,
不共线,且
=
+
,
=7
-2
,
=-5
+k
,A、B、C三点共线,求k值.
| a |
| b |
| AB |
| a |
| 2b |
| CD |
| a |
| b |
| BC |
| a |
| b |
考点:平行向量与共线向量
专题:平面向量及应用
分析:根据A、B、C三点共线,得出
=λ
(λ∈R),利用向量相等,求出k的值.
| BC |
| AB |
解答:
解:∵向量
,
不共线,且
=
+
,
=-5
+k
,A、B、C三点共线,
∴
=λ
(λ∈R),
∴-5
+k
=λ(
+2
),
即-5
+k
=λ
+2λ
;
∴
,
解得k=-10.
| a |
| b |
| AB |
| a |
| 2b |
| BC |
| a |
| b |
∴
| BC |
| AB |
∴-5
| a |
| b |
| a |
| b |
即-5
| a |
| b |
| a |
| b |
∴
|
解得k=-10.
点评:本题考查了利用平面向量判断三点共线的应用问题,是基础题目.

练习册系列答案
相关题目
点(x,y)的坐标x,y都是有理数时,该点称为有理点,在半径为r,圆心为(a,b)的圆中,若a∈Q,b∈Q,则这个圆上的有理点的数目为( )
| A、最多有一个 |
| B、最多有两个 |
| C、最多有三个 |
| D、可以有无穷多个 |
已知R上的可导函数f(x)满足f′(x)≤f(x)恒成立,若f(0)>0,则
的最大值为( )
| f(1) |
| f(0) |
| A、1 | B、e |
| C、e-1 | D、2e |
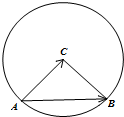 如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且
如图,定圆C半径为r,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且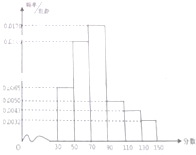 某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图:
某县为“中学生知识竞赛”进行选取性测试,规定:成绩大于或等于90分的右参赛资格,90分以下(不包括90分)的则被淘汰,若现有1000人参加测试,学生成绩的频率分别直方图如图: