题目内容
若
=
，则sinA+cosA的值为 ．
| sinA |
| 1+cosA |
| 1 |
| 2 |
考点：三角函数的化简求值
专题：三角函数的求值
分析：根据同角的三角函数的平方关系，先化简已知条件，求出cosA的值，再求出sinA的值，即可得出答案．
解答：
解：∵
=
，
∴2sinA=1+cosA，
两边平方，得4sin2A=1+2cosA+cos2A，
即4（1-cos2A）=1+2cosA+cos2A，
整理得，5cos2A+2cosA-3=0；
解得cosA=-1，或cosA=
；
当cosA=-1时，1+cosA=0，∴
无意义；
当cosA=
时，sinA=
=
=
；
∴sinA+cosA=
+
=
．
故答案为：
．
| sinA |
| 1+cosA |
| 1 |
| 2 |
∴2sinA=1+cosA，
两边平方，得4sin2A=1+2cosA+cos2A，
即4（1-cos2A）=1+2cosA+cos2A，
整理得，5cos2A+2cosA-3=0；
解得cosA=-1，或cosA=
| 3 |
| 5 |
当cosA=-1时，1+cosA=0，∴
| sinA |
| 1+cosA |
当cosA=
| 3 |
| 5 |
| 1+cosA |
| 2 |
1+
| ||
| 2 |
| 4 |
| 5 |
∴sinA+cosA=
| 4 |
| 5 |
| 3 |
| 5 |
| 7 |
| 5 |
故答案为：
| 7 |
| 5 |
点评：本题考查了同角的三角函数的求值问题，解题时应灵活地利用三角函数的基本关系进行解答，是基础题．
练习册系列答案
快捷英语周周练系列答案
相关题目
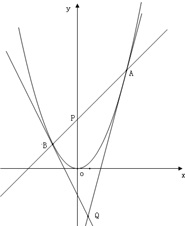已知A、B为抛物线C：x2=2y上的两点，点P（0，t）（t＞0）满足