题目内容
20．
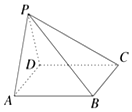如图，在四棱锥P-ABCD中，侧面PAD是边长为4的正三角形，底面ABCD为正方形，侧面PAD⊥底面ABCD，M为底面ABCD内的一个动点，且满足$\overrightarrow{MP}•\overrightarrow{MC}=0$，则点M到直线AB的最短距离为（ ）| A． | $\sqrt{5}$ | B． | $4-\sqrt{5}$ | C． | $3-\sqrt{5}$ | D． | $4-2\sqrt{2}$ |
分析 以D为原点，DA为x轴，DC为y轴，过D作平面ABCD的垂线为z轴，建立空间直角坐标系，利用向量法能求出点M到直线AB的最短距离．
解答 解：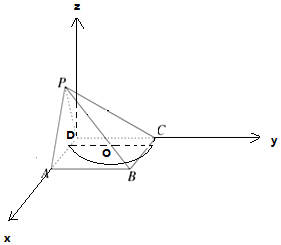
以D为原点，DA为x轴，DC为y轴，过D作平面ABCD的垂线为z轴，
建立空间直角坐标系，
则P（2，0，2$\sqrt{3}$），C（0，4，0），
设M（a，b，0），0≤a≤4，0≤b≤4，则$\overrightarrow{MP}$=（2-a，-b，2$\sqrt{3}$），$\overrightarrow{MC}$=（-a，4-b，0），
∵$\overrightarrow{MP}•\overrightarrow{MC}=0$，
∴$\overrightarrow{MP}•\overrightarrow{MC}$=-2a+a2-4b+b2=（a-1）2+（b-2）2=5，
∴M为底面ABCD内以O（1，2）为圆心，以r=$\sqrt{5}$为半径的圆上的一个动点，
∴点M到直线AB的最短距离为：4-1-$\sqrt{5}$=3-$\sqrt{5}$．
故选：C．
点评 本题考查点到直线的距离的最小值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
10．下列说法正确的是（ ）
| A． | 命题“若x2＞1，则x＞1”的否命题为“若x2＞1，则x≤1” | |
| B． | 命题“若$?{x_0}∈R，{x_0}^2＞1$”的否定是“?x∈R，x2＜1” | |
| C． | 命题“若x=y，则cosx=cosy”的逆否命题为假命题 | |
| D． | 命题“若x=y，则cosx=cosy”的逆命题为假命题 |
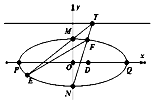已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的上顶点M与左、右焦点F1，F2构成三角形MF1F2面积为$\sqrt{3}$，又椭圆C的离心率为$\frac{{\sqrt{3}}}{2}$，左右顶点分别为P，Q．
交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为T，其范围分为五个级别，T∈[0，2）畅通；T∈[2，4）基本畅通； T∈[4，6）轻度拥堵；T∈[6，8）中度拥堵；T∈[8，10]严重拥堵．早高峰时段（T≥3），从某市交通指挥中心随机选取了三环以内的50个交通路段，依据其交通指数数据绘制的频率分布直方图如图．