题目内容
13.定义在R上的单调函数f(x)满足:f(x+y)=f(x)+f(y),若F(x)=f(asinx)+f(sinx+cos2x-3)在(0,π)上有零点,则a的取值范围是[2,+∞).分析 ①令x=y=0,则f(0)=2f(0),则f(0)=0;再令y=-x,f(x)+f(-x)=f(0)=0,可得f(x)是奇函数.
②F(x)=f(asinx)+f(sinx+cos2x-3)在(0,π)上有零点.f(-sinx-cos2x+3)在(0,π)上有解;根据函数f(x)是R上的单调函数,asinx=-sinx-cos2x+3在(0,π)上有解.x∈(0,π),sinx≠0;a=$\frac{-sinx-co{s}^{2}x+3}{sinx}$=sinx+$\frac{2}{sinx}$-1,令t=sinx,t∈(0,1];则a=t+$\frac{2}{t}$-1;利用导数研究其单调性即可得出.
解答 解:①令x=y=0,则f(0)=2f(0),则f(0)=0;
再令y=-x,则f(x-x)=f(x)+f(-x)=0,
且f(x)定义域为R,关于原点对称.
∴f(x)是奇函数.
②F(x)=f(asinx)+f(sinx+cos2x-3)在(0,π)上有零点.
∴f(asinx)+f(sinx+cos2x-3)=0在(0,π)上有解;
∴f(asinx)=-f(sinx+cos2x-3)=f(-sinx-cos2x+3)在(0,π)上有解;
又∵函数f(x)是R上的单调函数,
∴asinx=-sinx-cos2x+3在(0,π)上有解.
∵x∈(0,π),
∴sinx≠0;
∴a=$\frac{-sinx-co{s}^{2}x+3}{sinx}$=sinx+$\frac{2}{sinx}$-1;
令t=sinx,t∈(0,1];
则a=t+$\frac{2}{t}$-1;
∵y=t+$\frac{2}{t}$,${y}^{′}=1-\frac{2}{{t}^{2}}$<0,因此函数y在(0,1]上单调递减,
∴a≥2.
故答案为:[2,+∞).
点评 本题考查了抽象函数的奇偶性与单调性、三角函数求值、换元法、利用导数研究函数的单调性,考查了推理能力与计算能力,属于难题.

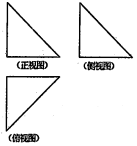 如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )
如图,一个空间几何体的正视图、侧视图、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为$\sqrt{2}$,那么这个几何体的体积是( )| A. | $\frac{{3+\sqrt{3}}}{2}$ | B. | $3+\sqrt{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{2}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |