题目内容
已知函数f(x)=x-
在定义域[1,20]上单调递增.
(1)求a的取值范围;
(2)若方程f(x)=10存在整数解,求满足条件a的个数.
| a |
| x |
(1)求a的取值范围;
(2)若方程f(x)=10存在整数解,求满足条件a的个数.
考点:函数单调性的性质
专题:函数的性质及应用
分析:(1)先求出函数的单调区间,得不等式
≤1,解出即可;
(2)问题转化为x2-10x+1≥0,解出x的范围,从而得出大于5+
,不大于20的整数有11个.
| -a |
(2)问题转化为x2-10x+1≥0,解出x的范围,从而得出大于5+
| 24 |
解答:
解:(1)∵f′(x)=1+
=
,
①a≥0时,f′(x)>0,f(x)在定义域递增,
②a<0时,令f′(x)>0,解得:x>
或x<-
,
∴f(x)在(-∞,-
)和(
,+∞)递增,
又∵f(x)的定义域是[1,20],
∴
≤1,解得:a≥-1,
综上:a≥-1;
(2)∵f(x)=x-
=10,
∴a=x2-10x≥-1.即x2-10x+1≥0,
解得:x<5-
(舍),x>5+
,
∴大于5+
,不大于20的x的整数有11个,
11个整数x代入就有11个相对应的a的值,
故满足条件的a的个数是11个.
| a |
| x2 |
| x2+a |
| x2 |
①a≥0时,f′(x)>0,f(x)在定义域递增,
②a<0时,令f′(x)>0,解得:x>
| -a |
| -a |
∴f(x)在(-∞,-
| -a |
| -a |
又∵f(x)的定义域是[1,20],
∴
| -a |
综上:a≥-1;
(2)∵f(x)=x-
| a |
| x |
∴a=x2-10x≥-1.即x2-10x+1≥0,
解得:x<5-
|
| 24 |
∴大于5+
| 24 |
11个整数x代入就有11个相对应的a的值,
故满足条件的a的个数是11个.
点评:本题考查了函数的单调性问题,考查了转化思想,是一道中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
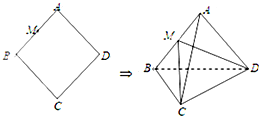 在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为
在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为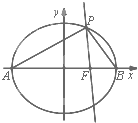 已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,AB=1,BC=2,PA=2,E、F分别是AB、PC的中点.