题目内容

已知正方体ABCD-A1B1C1D1，过点A、C及DD1延长线上一点G作出它的截面，其中D1G=
1
2
DD1，证明该截面为梯形．
考点：平面的基本性质及推论
专题：空间位置关系与距离
分析：如图所示，连接CG，AG，分别与C1D1，A1D1相交于F、E点，连接EF．利用正方体的性质、面面平行的性质定理可得：EF∥AC．D1E∥AD，
EG
AG
=
GD1
GD
=
1
2
，进而得出．
解答： 证明：如图所示，
连接CG，AG，分别与C1D1，A1D1相交于F、E点，连接EF．
∵平面ABCD∥平面A1B1C1D1，
∴EF∥AC．
∵D1E∥AD，
∴
EG
AG
=
GD1
GD
=
1
2
，
∴
EF
AC
=
1
2
．
∴该截面为梯形．
点评：本题考查了正方体的性质、面面平行的性质定理、平行线分线段成比例定理，考查了推理能力，属于基础题．
练习册系列答案
相关题目
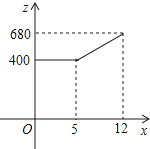我市某服装厂生产的服装供不应求，A车间接到生产一批西服的紧急任务，要求必须在12天内完成．为了加快进度，车间采取工人分批日夜加班，机器满负荷运转的生产方式，生产效率得到了提高，每天生产的西服数量y（套）与时间x（天）的关系如下表：
时间x（天）1234…
每天产量y（套）22242628…
平均每套西服的成本z（元）与时间x（天）的关系如图：
请解答下列问题．
（1）求每天生产的西服数量y（套）与x（天）之间的关系式及成本z（元）与x（天）之间的关系式．
（2）已知这批西服的订购价格为每套1400元，设该车间每天的利润为W（元），试求出日利润W（元）与时间x（天）之间的函数关系式，并求出哪一天该车间获得最大利润，最大利润是多少元？
（3）在实际销售中，厂家决定从第13天起，每天按日最大利润进行生产并完全售出．生产7天后，由于机器损耗等原因，平均每套西服的成本比日最大利润时增加0.5a%（a＜50），所以厂家把定购价提高了200元再生产8天，但这8天的日销量比日最大利润时的销量下降了a%，根据销售记录显示，这8天的销售利润的总和与前7天的销售利润总和持平，求整数a．
已知函数f（x）=x-
a
x
在定义域[1，20]上单调递增．
（1）求a的取值范围；
（2）若方程f（x）=10存在整数解，求满足条件a的个数．
在直角坐标系xOy中，圆C的参数方程
x=1+cosφ
y=sinφ
(φ为参数）．以O为极点，x轴的非负半轴为极轴建立极坐标系．
（Ⅰ）求圆C的极坐标方程；
（Ⅱ）直线l的极坐标方程是2ρsin(θ+
π
3
)=3
3
，射线OM：θ=
π
3
与圆C的交点为O、P，与直线l的交点为Q，求线段PQ的长．
如图，四棱锥P-ABCD中，△PAB是正三角形，四边形ABCD是矩形，且平面PAB⊥平面ABCD，PA=2，PC=4．
（Ⅰ）若点E是PC的中点，求证：PA∥平面BDE；
（Ⅱ）若点F在线段PA上，且FA=λPA，当三棱锥B-AFD的体积为
4
3
时，求实数λ的值．
已知椭圆
x2
a2
+
y2
16
=1，离心率为
3
5
．
（Ⅰ）求椭圆的方程；
（Ⅱ）过a＞4的椭圆的右焦点F任作一条斜率为k（k≠0）的直线交椭圆于A，B两点，问在F右侧是否存在一点D（m，0），连AD、BD分别交直线x=
25
3
于M，N两点，且以MN为直径的圆恰好过F，若存在，求m的值；若不存在，请说明理由．
已知圆锥的表面积为9πcm2，且它的侧面展开图是一个半圆，则圆锥的底面半径为（　　）
A、
3
2
2
cm
B、3
2
cm
C、
3
cm
D、2
3
cm
已知函数f（x）=
1+lnx
x
．
（Ⅰ）若函数f（x）在区间（m，m+
1
3
）（m＞0）上存在极值，求实数m的取值范围；
（Ⅱ）设g（x）=
1+x
a(1-x)
[xf（x）-1]，若对任意x∈（0，1）恒有g（x）＜-2，求实数a的取值范围．
函数f（x）=
1
2
sin（ωx-
π
3
）（ω＞0）的图象在[
π
4
，
π
2
]上为增函数，则ω的取值范围为（　　）
A、[
2
3
，
5
3
]
B、[
17
3
，
22
3
]
C、(0，
5
3
]
D、(0，
17
3
]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网