题目内容
一列火车在平直的铁轨上行驶,由于遇到紧急情况,火车以速度v(t)=5-t+
(t的单位:s,v的单位:m/s)紧急刹车至停止.则从开始紧急刹车至火车完全停止所经过的时间等于 (s);紧急刹车后火车运行的路程等于 (m).
| 55 |
| 1+t |
考点:函数的最值及其几何意义
专题:计算题
分析:(1)令v(t)=0,解得的根就是从开始紧急刹车至火车完全停止所经过的时间.
(2)紧急刹车后火车运行的路程就是t从0到10对函数v(t)=5-t+
的定积分.
(2)紧急刹车后火车运行的路程就是t从0到10对函数v(t)=5-t+
| 55 |
| 1+t |
解答:
解:(1)当火车的速度v=0时火车完全停止,即5-t+
=0,
∴t2-4t-60=0,解得t=10或t=-6(舍去).
即从开始紧急刹车至火车完全停止所经过的时间为10s.
故答案为:10;
(2)根据定积分的物理意义,紧急刹车后火车运行的路程就是t从0到10对函数
v(t)=5-t+
的定积分,
令 F(t)=5t-
t2+55ln(1+t)则F′(t)=v(t)=5-t+
∴S=∫010 v(t)dt═∫010(5-t+
)dt=F(10)-F(0)=55×ln11=55ln11
故答案为:55ln11
| 55 |
| 1+t |
∴t2-4t-60=0,解得t=10或t=-6(舍去).
即从开始紧急刹车至火车完全停止所经过的时间为10s.
故答案为:10;
(2)根据定积分的物理意义,紧急刹车后火车运行的路程就是t从0到10对函数
v(t)=5-t+
| 55 |
| 1+t |
令 F(t)=5t-
| 1 |
| 2 |
| 55 |
| 1+t |
∴S=∫010 v(t)dt═∫010(5-t+
| 55 |
| 1+t |
故答案为:55ln11
点评:本题主要考查定积分的物理意义,只要找对被积函数的原函数即可.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
方程ln(x+1)-
=0,(x>0)的根存在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
抛物线y=2ax2(a≠0)焦点坐标是( )
A、(
| ||
B、(0,
| ||
C、(
| ||
D、(0,
|
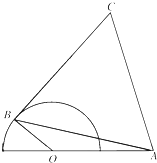 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.