题目内容
已知an=
（n∈N*），则当n= 时，an最大，n= 时，an最小．
n-
| ||
n-
|
考点：数列的函数特性
专题：函数的性质及应用
分析：由于an=
=1+
，44＜
＜45．可得：当n≤44时，an＜1，{an}单调递减；当n≥45时，an＞1，{an}单调递减．
n-
| ||
n-
|
| ||||
n-
|
| 2008 |
解答：
解：an=
=
=1+
，
∵44＜
＜45．
当n≤44时，an＜1，{an}单调递减；当n≥45时，an＞1，{an}单调递减．
∴当n=45时，an最大；当n=44时，an最小．
故答案为：45，44．
n-
| ||
n-
|
n-
| ||||||
n-
|
| ||||
n-
|
∵44＜
| 2008 |
当n≤44时，an＜1，{an}单调递减；当n≥45时，an＞1，{an}单调递减．
∴当n=45时，an最大；当n=44时，an最小．
故答案为：45，44．
点评：本题考查了数列的单调性，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
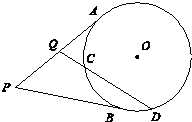如图，p为⊙O外一点，过P点作⊙O的两条切线，切点分别为A，B，过PA的中点Q作割线交⊙O于C，D两点，若QC=1，CD=4，则PB=
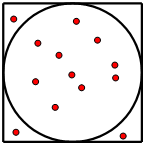某同学动手做实验：《用随机模拟的方法估计圆周率的值》，在左下图的正方形中随机撒豆子，每个豆子落在正方形内任何一点是等可能的，若他随机地撒50粒统计得到落在圆内的豆子数为35粒，则由此估计出的圆周率π的值为