题目内容
已知圆心在直线2x-y-3=0上,且过点A(5,2)和点B(3,2),则圆C的方程为 .
考点:圆的标准方程
专题:直线与圆
分析:设圆心C(a,b),由已知,得:
,由此能求出圆C的方程.
|
解答:
解:设圆心C(a,b),
由已知,得:
,
解得a=4,b=5,
∴圆心C(4,5),
半径r=
=
,
∴圆C的方程为(x-4)2+(y-5)2=10.
故答案为:(x-4)2+(y-5)2=10.
由已知,得:
|
解得a=4,b=5,
∴圆心C(4,5),
半径r=
| (4-5)2+(5-2)2 |
| 10 |
∴圆C的方程为(x-4)2+(y-5)2=10.
故答案为:(x-4)2+(y-5)2=10.
点评:本题考查圆的方程的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设直线过点(0,a),其斜率为1,且与圆x2+y2=4相切,则a的值为( )
| A、±4 | ||
B、±2
| ||
| C、4x+2y=5 | ||
| D、4x-2y=5 |
由y=ex、x轴、y轴及直线x=2围成的封闭图形的面积为( )
| A、e2 |
| B、e2-1 |
| C、e2+1 |
| D、e2ln2-1 |
已知直线ax+by-1=0(a>0,b>0)过圆x2+y2-4x-2y=0的圆心,则
+
的最小值为( )
| 1 |
| a |
| 1 |
| 2b |
A、
| ||
B、
| ||
C、
| ||
D、
|

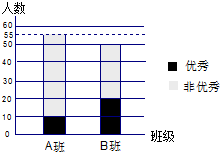 中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.
中山纪念中学高二A、B两个班参加了2012年的“广州一模数学考试”,按照成绩大于等于125分为“优秀”,成绩小于125分为“非优秀”,根据调查这两个班的数学成绩得到的数据,所绘制的二维条形图如图.