题目内容
20.已知P(xp,5)是双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$(a>0,b>0)上的一点,F1,F2分别是双曲线的左,右焦点,若|PF1|•|PF2|=$\frac{9}{4}$ac,△PF1F2的内切圆的面积为4π,则双曲线Γ的渐近线方程为( )| A. | y=$±\sqrt{2}$x | B. | y=±$\frac{\sqrt{7}}{3}$x | C. | y=±$\frac{4}{3}$x | D. | y=±$\sqrt{6}$x |
分析 设|PF1|=m,|PF2|=n(m>n),则$\frac{1}{2}×2c×5$=$\frac{1}{2}×(m+n+2c)×2$,结合双曲线的定义,求出m,n,再利用|PF1|•|PF2|=$\frac{9}{4}$ac,求出e,即可得出结论.
解答 解:设|PF1|=m,|PF2|=n(m>n),则$\frac{1}{2}×2c×5$=$\frac{1}{2}×(m+n+2c)×2$,
∴m+n=3c,
∵m-n=2a,
∴m=$\frac{3}{2}$c+a,n=$\frac{3}{2}$c-a,
∵|PF1|•|PF2|=$\frac{9}{4}$ac,
∴($\frac{3}{2}$c+a)•($\frac{3}{2}$c-a)=$\frac{9}{4}$ac,
∴$\frac{9}{4}$e2-$\frac{9}{4}$e-1=0,
∴e=$\frac{4}{3}$,
∴$\frac{b}{a}$=$\frac{\sqrt{7}}{3}$.
∴双曲线Γ的渐近线方程为y=±$\frac{\sqrt{7}}{3}$x.
故选:B.
点评 本题考查双曲线的方程与性质,考查双曲线的定义,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
8.如图,ABCD-A1B1C1D1为正方体,下面结论错误的是( )
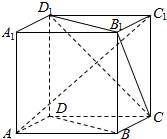

| A. | BD∥平面CB1D1 | B. | AC1⊥BD | ||
| C. | 异面直线AD与CB1角为60° | D. | AC1⊥平面CB1D1 |
12.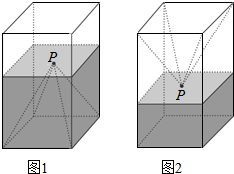 如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个结论,其中错误的代号是( )
如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个结论,其中错误的代号是( )
 如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个结论,其中错误的代号是( )
如图1,一个正四棱柱形的密闭容器水平放置,其底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个结论,其中错误的代号是( )| A. | 若往容器内再注入a升水,则容器恰好能装满 | |
| B. | 将容器侧面水平放置时,水面也恰好过点P | |
| C. | 任意摆放该容器,当水面静止时,水面都恰好经过点P | |
| D. | 正四棱锥的高等于正四棱柱高的一半 |
9.与圆O1:x2+y2=1和圆O2:x2+y2-6x-8y+9=0都相切的直线条数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.“x≥0”是“log${\;}_{\frac{1}{2}}$(x+2)<2”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |