题目内容
15.已知双曲线C经过点(2,2),且与$\frac{{y}^{2}}{4}$-x2=1具有相同渐近线,求双曲线C的方程.分析 与$\frac{{y}^{2}}{4}$-x2=1有相同的渐近线的方程可设为$\frac{{y}^{2}}{4}$-x2=λ≠0,再把点P的坐标代入即可.
解答 解:依题设所求双曲线方程为$\frac{{y}^{2}}{4}$-x2=λ≠0,
∵双曲线过点P(2,2),
∴1-4=λ,
∴λ=-3
∴所求双曲线方程为$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{12}=1$.
点评 本题考查双曲线方程的求法,正确利用:与$\frac{{y}^{2}}{4}$-x2=1有相同的渐近线的方程可设为$\frac{{y}^{2}}{4}$-x2=λ≠0,是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
6.若点(2a,a+1)在圆x2+(y-1)2=5的内部,则a的取值范围是( )
| A. | (-1,1) | B. | (0,1) | C. | (-1,$\frac{1}{5}$) | D. | (-$\frac{1}{5}$,1) |
3.经过平面外一点与平面垂直的平面有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
20.已知P(xp,5)是双曲线Γ:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$(a>0,b>0)上的一点,F1,F2分别是双曲线的左,右焦点,若|PF1|•|PF2|=$\frac{9}{4}$ac,△PF1F2的内切圆的面积为4π,则双曲线Γ的渐近线方程为( )
| A. | y=$±\sqrt{2}$x | B. | y=±$\frac{\sqrt{7}}{3}$x | C. | y=±$\frac{4}{3}$x | D. | y=±$\sqrt{6}$x |
4.幂函数y=xm(m∈Z)的图象如图所示,则m的值可以为( )


| A. | 1 | B. | -1 | C. | -2 | D. | 2 |
5.已知一组数据为1、5、6、2、6,则这组数据的众数、中位数、平均数的大小关系为( )
| A. | 中位数>平均数>众数 | B. | 众数>中位数>平均数 | ||
| C. | 众数>平均数>中位数 | D. | 平均数>众数>中位数 |
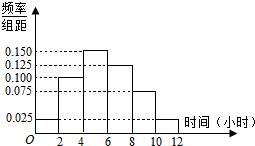 某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).
某校共有学生1600人,其中男生1000人,女生600人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集40位学生每周平均体育运动时间的样本数据(单位:小时).