题目内容
17.函数y=f(x)的定义域为[-1,5],则函数y=f(2x2-1)的定义域为( )| A. | [-1,5] | B. | [0,3] | C. | [-$\sqrt{3}$,$\sqrt{3}$] | D. | [1,49] |
分析 利用抽象函数的定义域,求解函数的定义域即可.
解答 解:函数y=f(x)的定义域为[-1,5],可得-1≤2x2-1≤5,
解得x∈[-$\sqrt{3}$,$\sqrt{3}$].
故选:C.
点评 本题考查函数的定义域的求法,考查计算能力.

练习册系列答案
相关题目
8.下列函数f(x),g(x)表示同一个函数的是( )
| A. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(x)=x+1 | B. | f(x)=lnex与g(x)=elnx | ||
| C. | f(x)=|x|与g(x)=$\sqrt{{x}^{2}}$ | D. | f(x)=$\sqrt{x-1}$•$\sqrt{x+1}$与g(x)=$\sqrt{{x}^{2}-1}$ |
20.已知函数f(x)=lg(x+2),若0<c<b<a,则 $\frac{f(a)}{a}$、$\frac{f(b)}{b}$、$\frac{f(c)}{c}$的大小关系为( )
| A. | $\frac{f(a)}{a}$>$\frac{f(b)}{b}$>$\frac{f(c)}{c}$ | B. | $\frac{f(c)}{c}$>$\frac{f(b)}{b}$>$\frac{f(a)}{a}$ | C. | $\frac{f(b)}{b}$>$\frac{f(a)}{a}$>$\frac{f(c)}{c}$ | D. | $\frac{f(a)}{a}$>$\frac{f(c)}{c}$>$\frac{f(b)}{b}$ |
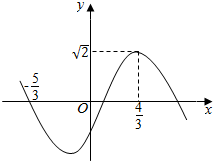 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示.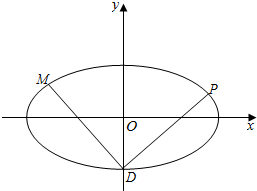 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到右准线的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.