题目内容
若圆C1:x2+y2-2tx+t2-4=0与圆C2:x2+y2+2x-4ty+4t2-8=0相交,则t的取值范围是( )
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
考点:圆与圆的位置关系及其判定
专题:直线与圆
分析:根据这两个圆相交,可得圆心距大于半径之差而小于半径之和,可得3-2<
<3+2,即0<5t2+2t<24,由此求得t的取值范围.
| (t+1)2+(0-2t)2 |
解答:
解:圆C1:x2+y2-2tx+t2-4=0即 (x-t)2+y2=4,表示以C1(t,0)为圆心、半径等于2的圆;
圆C2:x2+y2+2x-4ty+4t2-8=0即 (x+1)2+(y-2t)2=9,表示以C2(-1,2t)为圆心、半径等于3的圆.
再根据这两个圆相交,可得圆心距大于半径之差而小于半径之和,
即 3-2<
<3+2,即0<5t2+2t<24,
∴
,
解得-
<t<-
或0<t<2,
故选:D.
圆C2:x2+y2+2x-4ty+4t2-8=0即 (x+1)2+(y-2t)2=9,表示以C2(-1,2t)为圆心、半径等于3的圆.
再根据这两个圆相交,可得圆心距大于半径之差而小于半径之和,
即 3-2<
| (t+1)2+(0-2t)2 |
∴
|
解得-
| 12 |
| 5 |
| 2 |
| 5 |
故选:D.
点评:本题主要考查圆的标准方程,两圆的位置关系的判定方法,两点间的距离公式的应用,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
若直线l1:x+(1+m)y=2-m与直线l2:2mx+4y=-16平行,则m=( )
| A、m=-2 | ||
| B、m=1 | ||
| C、m=-2或 m=1 | ||
D、-
|
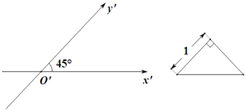 已知一个三棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如右图所示),则此三棱锥的体积为( )
已知一个三棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如右图所示),则此三棱锥的体积为( )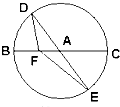 如图,BC是单位圆A的一条直径,F是线段AB上的点,且
如图,BC是单位圆A的一条直径,F是线段AB上的点,且