题目内容
10．已知M是抛物线C：y2=2px（p＞0）上一点，F是抛物线C的焦点，若|MF|=p，K是抛物线C的准线与x轴的交点，则∠MKF=（ ）| A． | 45° | B． | 30° | C． | 15° | D． | 60° |
分析 设点M（$\frac{p}{2}$，p），K（-$\frac{p}{2}$，0），则直线KM的斜率k=1，即可求得∠MKF=45°．
解答 解：由题意，|MF|=p，则设点M（$\frac{p}{2}$，p），
∵K（-$\frac{p}{2}$，0），
∴kKM=1，
∴∠MKF=45°，
故选A．
点评 本题考查抛物线的简单几何性质，直线的斜率公式，属于基础题．
练习册系列答案
相关题目
1．设a∈R，“1，a，16为等比数列”是“a=4”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |
5．若函数f（x）=（ax2+bx）ex的图象如图所示，则实数a，b的值可能为（ ）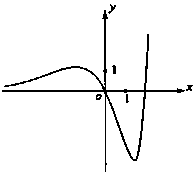
| A． | a=1，b=2 | B． | a=1，b=-2 | C． | a=-1，b=2 | D． | a=-1，b=-2 |
15．
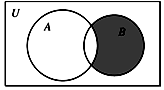设全集U=N*，集合A={1，2，3，5}，B={2，4，6}，则图中的阴影部分表示的集合为（ ）
设全集U=N*，集合A={1，2，3，5}，B={2，4，6}，则图中的阴影部分表示的集合为（ ）| A． | {2} | B． | {4，6} | C． | {1，3，5} | D． | {2，4，6} |
19．斜率为k（k＞0）的直线经过抛物线y2=2px（p＞0）的焦点，与抛物线交于A、B两点，与抛物线的准线交于C点，当B为AC中点时，k的值为（ ）
| A． | $\frac{\sqrt{2}}{4}$ | B． | $\sqrt{2}$ | C． | 2$\sqrt{2}$ | D． | 3$\sqrt{2}$ |
1．设集合A={x|$\frac{x+1}{1-x}$＞0}，B={x|x+2≥0}，则A∩B=（ ）
| A． | {x|-1＜x＜1} | B． | {x|x≥-2} | C． | {x|-2≤x＜1} | D． | {x|-1＜x≤2} |