题目内容
国家标准规定:轻型汽车的氮氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取6辆,对其氮氧化物的排放量进行检测,检测结果记录如下:(单位:mg/km)
由于表格被污损,数据x看不清,统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等.
(1)求表格中x的值;
(2)从被检测的6辆B种型号的出租车中任取3辆,记事件A:至少有两辆出租车氮氧化物排放量未超过80mg/km,求事件A的概率.
| A | 85 | 80 | 85 | 60 | 90 | 80 |
| B | 70 | 85 | 95 | x | 75 | 65 |
(1)求表格中x的值;
(2)从被检测的6辆B种型号的出租车中任取3辆,记事件A:至少有两辆出租车氮氧化物排放量未超过80mg/km,求事件A的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)根据A、B两种出租车的氮氧化物排放量的平均值相等,可得两组数据的总和相等,进而可得表格中x的值;
(2)分别计算出被检测的6辆B种型号的出租车中任取3辆的基本事件总数和满足至少有两辆出租车氮氧化物排放量未超过80mg/km的基本事件个数,代入古典概型概率计算公式,可得答案.
(2)分别计算出被检测的6辆B种型号的出租车中任取3辆的基本事件总数和满足至少有两辆出租车氮氧化物排放量未超过80mg/km的基本事件个数,代入古典概型概率计算公式,可得答案.
解答:
解:(1)∵A、B两种出租车的氮氧化物排放量的平均值相等,
∴85+80+85+60+90+80=70+80+95+x75+70,
解得:x=90.
(2)从被检测的6辆B种型号的出租车中任取3辆,共有
=20种不同情况;
由事件A:至少有两辆出租车氮氧化物排放量未超过80mg/km得:
A中共包含:
•
=9+1=10种不同情况,
故P(A)=
=
,
故从被检测的6辆B种型号的出租车中任取3辆,至少有两辆出租车氮氧化物排放量未超过80mg/km的概率为
.
∴85+80+85+60+90+80=70+80+95+x75+70,
解得:x=90.
(2)从被检测的6辆B种型号的出租车中任取3辆,共有
| C | 3 6 |
由事件A:至少有两辆出租车氮氧化物排放量未超过80mg/km得:
A中共包含:
| C | 2 3 |
| C | 1 3 |
| +C | 3 3 |
故P(A)=
| 10 |
| 20 |
| 1 |
| 2 |
故从被检测的6辆B种型号的出租车中任取3辆,至少有两辆出租车氮氧化物排放量未超过80mg/km的概率为
| 1 |
| 2 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
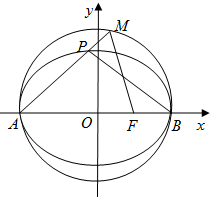 已知椭圆C:
已知椭圆C: 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.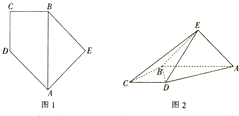 已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连接EC、ED,得到四棱锥E-ABCD(如图2).
已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连接EC、ED,得到四棱锥E-ABCD(如图2).