题目内容
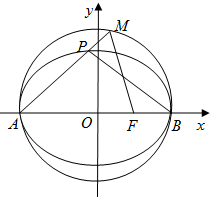 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)点M(x0,y0)(x0≠1,y0>0)是圆O:x2+y2=a2上的任意一点,连结AM,交椭圆C于P,记直线MF,PB的斜率分别为k1,k2.
①当k2=-
| 3 |
| 4 |
②求
| k1 |
| k2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出
,由此能求出椭圆C的方程.
(Ⅱ)①由题意知M(x0,y0),(x0≠1,y0>0),A(-2,0),B(2,0),F(1,0),P(2cosθ,
sinθ),从而得到k1=
,k2=
=-
,x02+y02=4,由此能求出k1.
②设PA的斜率为k3,则k3=
=
,由此得到
=
=
=-
(-1+
),从而利用x0∈(-2,1)∪(1,2),能求出
∈(-∞,0)∪(
,+∞).
|
(Ⅱ)①由题意知M(x0,y0),(x0≠1,y0>0),A(-2,0),B(2,0),F(1,0),P(2cosθ,
| 3 |
| y0 |
| x0-1 |
| ||
| 2cosθ-2 |
| 3 |
| 4 |
②设PA的斜率为k3,则k3=
| ||
| 2cosα+2 |
| y0 |
| x0+2 |
| k1 |
| k2 |
| k1k3 |
| k2k3 |
| ||||
-
|
| 4 |
| 3 |
| 1 |
| x0-1 |
| k1 |
| k2 |
| 16 |
| 9 |
解答:
 解:(Ⅰ)∵椭圆C:
解:(Ⅰ)∵椭圆C:
+
=1(a>b>0)的右焦点为F,
离心率为
,且椭圆经过定点(
,
),
∴
,解得a2=4,b2=3,
∴椭圆C的方程为
+
=1.…(4分)
(Ⅱ)①由题意知M(x0,y0),(x0≠1,y0>0),
A(-2,0),B(2,0),F(1,0),P(2cosθ,
sinθ),
∴k1=
,k2=
=-
,x02+y02=4,
解得cosθ=-
,或cosθ=1(舍),∴sinθ=
,
∵点P在直线AM上,∴
=
,
解得x0=0,y0=2,或x0=-2,y0=0(舍),
∴k1=
=
=-2.…(8分)
②设PA的斜率为k3,则k3=
=
,
∴k2k3=
•
=-
,
∴
=
=
=-
•
•
=-
•
=-
(-1+
),
∵x0∈(-2,1)∪(1,2),
∴
∈(-∞,0)∪(
,+∞).…(16分)
 解:(Ⅰ)∵椭圆C:
解:(Ⅰ)∵椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
离心率为
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴
|
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)①由题意知M(x0,y0),(x0≠1,y0>0),
A(-2,0),B(2,0),F(1,0),P(2cosθ,
| 3 |
∴k1=
| y0 |
| x0-1 |
| ||
| 2cosθ-2 |
| 3 |
| 4 |
解得cosθ=-
| 1 |
| 7 |
4
| ||
| 7 |
∵点P在直线AM上,∴
| ||
| 2cosθ+2 |
| y0 |
| x0+2 |
解得x0=0,y0=2,或x0=-2,y0=0(舍),
∴k1=
| y0 |
| x0-1 |
| 2 |
| 0-1 |
②设PA的斜率为k3,则k3=
| ||
| 2cosα+2 |
| y0 |
| x0+2 |
∴k2k3=
| ||
| 2cosθ-2 |
| ||
| 2cosθ+2 |
| 3 |
| 4 |
∴
| k1 |
| k2 |
| k1k3 |
| k2k3 |
| ||||
-
|
| 4 |
| 3 |
| y0 |
| x0-1 |
| y0 |
| x0+2 |
=-
| 4 |
| 3 |
| 2-x0 |
| x0-1 |
| 4 |
| 3 |
| 1 |
| x0-1 |
∵x0∈(-2,1)∪(1,2),
∴
| k1 |
| k2 |
| 16 |
| 9 |
点评:本题考查椭圆方程的求法,考查直线斜率的求法,考查两直线斜率的比值的取值范围的求法,解题时要认真审题,注意椭圆的参数方程的合理运用.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知数列{an},an+1=kan+3(k>0),其中a1=0,a4=9,则k等于( )
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
在△ABC中,角A,B,C所对的边分别为5,7,8,则∠B的大小是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若点A(1,m-1,1)和点B(-1,-3,-1)关于原点对称,则m=( )
| A、-4 | B、4 | C、2 | D、-2 |
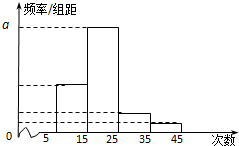 对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,
对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,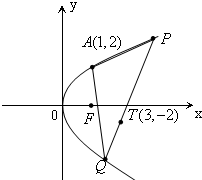 点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点
点A(1,2)到抛物线y2=2px(p>0)的焦点F的距离为2,过T(3,-2)的动直线l与此抛物线交于P、Q两点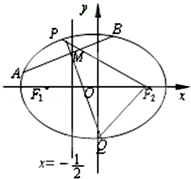 如图,F1,F2是离心率为
如图,F1,F2是离心率为