题目内容
△ABC中,已知A(-2,11),B(-4,5),C(6,0),求点A在BC上的投影坐标.
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:求出BC的斜率与方程,求出过A与BC垂直的直线方程,通过求解交点即可.
解答:
解:B(-4,5),C(6,0),
∴kBC=
=-
,
∴BC的方程为:y=-
(x-6),即x+2y-6=0.
过A与BC垂直的直线方程:y-11=2(x+2),即:2x-y+15=0.
由
解得
,
∴点A在BC上的投影坐标(
,
).
∴kBC=
| 5-0 |
| -4-6 |
| 1 |
| 2 |
∴BC的方程为:y=-
| 1 |
| 2 |
过A与BC垂直的直线方程:y-11=2(x+2),即:2x-y+15=0.
由
|
|
∴点A在BC上的投影坐标(
| 3 |
| 5 |
| 27 |
| 5 |
点评:本题考查直线方程的求法,直线与直线的垂直关系的应用,基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
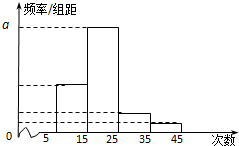 对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图,
对某校高二年级学生中学阶段参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图, 已知△ABC是边长为3的等边三角形,点D、E分别是边AB,AC上的点,且满足
已知△ABC是边长为3的等边三角形,点D、E分别是边AB,AC上的点,且满足 如图,设D是图中边长为2的正方形区域,E是函数y=x3的 图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为
如图,设D是图中边长为2的正方形区域,E是函数y=x3的 图象与x轴及x=±1围成的阴影区域.向D中随机投一点,则该点落入E中的概率为