题目内容
在三棱锥S-ABC中,侧棱SA,SB,SC两两垂直,且SA=a,SB=b,SC=c,现有下列命题:
①△ABC一定为锐角三角形;
②该三棱锥的每组对棱分别互相垂直;
③该三棱锥的外接球的半径为
;
④顶点S在平面ABC内的射影一定为△ABC的重心.
其中真命题有 (填上你认为的真命题的序号)
①△ABC一定为锐角三角形;
②该三棱锥的每组对棱分别互相垂直;
③该三棱锥的外接球的半径为
| a2+b2+c2 |
④顶点S在平面ABC内的射影一定为△ABC的重心.
其中真命题有
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:分别根据三棱锥的性质,以及空间直线的位置关系进行判断即可得到结论.
解答:
解:①∵SA⊥SB,SA⊥SC,
∴SA⊥平面SBC,BC?平面SBC.∴SA⊥BC.
而AD是SA在平面ABC上的射影,∴AD⊥BC.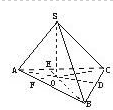
同理可证AB⊥CF,AC⊥BE,故O为△ABC的垂心,故①②正确,④错误.
③以SA,SB,SC为棱构造长方体,则长方体的体对角线为三棱锥的外接球的直径,
则2r=
,即外接圆的半径r=
,故③错误.
故正确的命题为①②,
故答案为:①②
∴SA⊥平面SBC,BC?平面SBC.∴SA⊥BC.
而AD是SA在平面ABC上的射影,∴AD⊥BC.

同理可证AB⊥CF,AC⊥BE,故O为△ABC的垂心,故①②正确,④错误.
③以SA,SB,SC为棱构造长方体,则长方体的体对角线为三棱锥的外接球的直径,
则2r=
| a2+b2+c2 |
| 1 |
| 2 |
| a2+b2+c2 |
故正确的命题为①②,
故答案为:①②
点评:本题主要考查空间三棱锥的位置关系的判断,涉及的知识点较多,综合性较强.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
已知在全部105人中随机抽取1人,成绩优秀的概率为
,则下列说法正确的是( )
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | b | |
| 乙班 | c | 30 | |
| 总计 | 105 |
| 2 |
| 7 |
| A、列联表中c的值为30,b的值为35 |
| B、列联表中c的值为15,b的值为50 |
| C、根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系” |
| D、根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系” |
已知点F(c,0)(c>0)是双曲线
-
=1的右焦点,F关于直线y=
x的对称点A恰在该双曲线的右支上,则该双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 某校为了解高三男生的身体状况,检测了全部480名高三男生的体重(单位:kg),所得数据都在区间[50,75]中,其频率分布直方图如图所示.若图中从左到右的前3个小组的频率之比为1:2:3,则体重小于60kg的高三男生人数为
某校为了解高三男生的身体状况,检测了全部480名高三男生的体重(单位:kg),所得数据都在区间[50,75]中,其频率分布直方图如图所示.若图中从左到右的前3个小组的频率之比为1:2:3,则体重小于60kg的高三男生人数为