题目内容
13.在等差数列{an}中,a1=-2008,其前n项和为Sn,若$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=2,则S2008的值等于-2008.分析 根据等差数列的前n项和的公式分别求出S12和S10的值,将其值代入到$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=2中即可求出公差d,然后根据首项为-2008,公差为2算出S2008的值即可.
解答 解:因为S12=12×(-2008)+66d,S10=10×(-2008)+45d,
则$\frac{{S}_{12}}{12}$-$\frac{{S}_{10}}{10}$=d=2,
则S2008=2008×(-2008)+$\frac{2008×2007}{2}$×2=2008×(-2008+2007)=-2008.
故答案为-2008.
点评 考查学生灵活运用等差数列的前n项和的公式化简求值,解题的关键是求数列的公差.

练习册系列答案
相关题目
4.某三棱锥的三视图是三个边长相等的正方形及对角线,若该几何体的体积是$\frac{1}{3}$,则它的表面积是( )
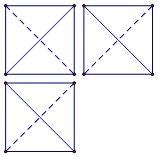

| A. | 1 | B. | 2 | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
18.已知$f(x)=\frac{{{x^2}+33}}{x}(x∈{N^*})$,则f(x)在定义域上的最小值为( )
| A. | $\frac{58}{5}$ | B. | $\frac{23}{2}$ | C. | $\sqrt{33}$ | D. | $2\sqrt{33}$ |
5.设复数z满足z(1+i)=2,i为虚数单位,则复数z的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
2.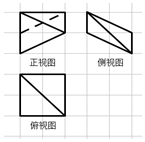 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
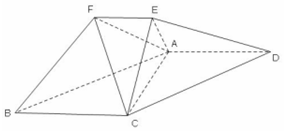 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,