题目内容
14.已知抛物线C:y2=4x的焦点为F,过F的直线l交C于A,B两点,M为线段AB的中点,O为坐标原点.AO、BO的延长线与直线x=-4分别交于P、Q两点.(Ⅰ)求动点M的轨迹方程;
(Ⅱ)连接OM,求△OPQ与△BOM的面积比.
分析 (1)先根据抛物线方程求得焦点坐标,进而设出过焦点弦的直线方程,与抛物线方程联立消去y,根据韦达定理表示出x1+x2,进而根据直线方程求得y1+y2,进而求得焦点弦的中点的坐标的表达式,消去参数k,则焦点弦的中点轨迹方程可得.
(2)求出P,Q的坐标,可得面积,即可求△OPQ与△BOM的面积比.
解答 解:(Ⅰ)设A (x1,y1),B(x2,y2),由题知抛物线焦点为(1,0)
设焦点弦方程为y=k(x-1)
代入抛物线方程得所以k2x2-(2k2+4)x+k2=0
由韦达定理:x1+x2=2+$\frac{4}{{k}^{2}}$
所以中点M横坐标:x=1+$\frac{2}{{k}^{2}}$
代入直线方程,中点M纵坐标:y=k(x-1)=$\frac{2}{k}$.即中点M为(1+$\frac{2}{{k}^{2}}$,$\frac{2}{k}$)
消参数k,得其方程为:y2=2x-2,
当线段PQ的斜率不存在时,线段PQ中点为焦点F(1,0),满足此式,
故动点M的轨迹方程为:y2=2x-2…(6分)
(Ⅱ)设AB:ky=x-1,代入y2=4x,得y2-4ky-4=0,
y1+y2=4k,y1•y2=-4,
联立,得P(-4,-$\frac{16}{{y}_{1}}$),同理Q(-4,-$\frac{16}{{y}_{2}}$),…(9分)
|PQ|=4|y1-y2|,
∴S△OPQ=8|y1-y2|,
又∵S△OMB=$\frac{1}{4}$|y1-y2|,故△OPQ与△BOM的面积比为32.…(12分)
点评 本题主要考查了抛物线的简单性质,考查直线与抛物线的位置关系,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
4.某三棱锥的三视图是三个边长相等的正方形及对角线,若该几何体的体积是$\frac{1}{3}$,则它的表面积是( )
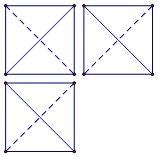

| A. | 1 | B. | 2 | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
5.设复数z满足z(1+i)=2,i为虚数单位,则复数z的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
2.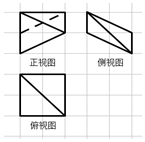 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
 如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )
如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 4 |
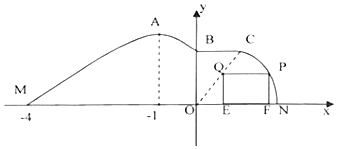 “中国齐云山国际养生万人徒步大会”得到了国内外户外运动爱好者的广泛关注,为了使基础设施更加完善,现需对部分区域进行改造.如图,在道路 北侧准备修建一段新步道,新步道开始部分的曲线段MAB是函数y=2sin(ωx+ϕ),(ω>0,0<ϕ<π),x∈[-4,0]的图象,且图象的最高点为A(-1,2).中间部分是长为1千米的直线段BC,且BC∥MN.新步道的最后一部分是以原点O为圆心的一段圆弧CN.
“中国齐云山国际养生万人徒步大会”得到了国内外户外运动爱好者的广泛关注,为了使基础设施更加完善,现需对部分区域进行改造.如图,在道路 北侧准备修建一段新步道,新步道开始部分的曲线段MAB是函数y=2sin(ωx+ϕ),(ω>0,0<ϕ<π),x∈[-4,0]的图象,且图象的最高点为A(-1,2).中间部分是长为1千米的直线段BC,且BC∥MN.新步道的最后一部分是以原点O为圆心的一段圆弧CN.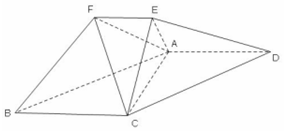 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD 为平行四边形,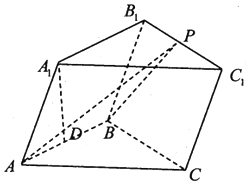 在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.
在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.