Question

11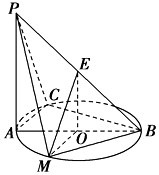．如图所示，PA⊥平面ABC，点C在以AB为直径的⊙O上，∠CBA=30°，PA=AB=2，点E为线段PB的中点，点M在$\widehat{AB}$上，且OM∥AC．
（Ⅰ）求证：平面MOE∥平面PAC；
（Ⅱ）求证：平面PAC⊥平面PCB．

Answer 1

分析 （1）推导出OE∥PA，从而OE∥平面PAC，由OM∥AC，得OM∥平面PAC．由此能证明平面MOE∥平面PAC．
（2）推导出BC⊥AC，PA⊥BC，从而BC⊥平面PAC．由此能证明平面PAC⊥平面PBC．

解答 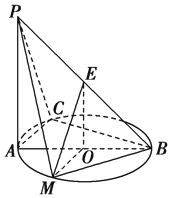（本小题满分10分）
证明：（1）因为点E为线段PB的中点，点O为线段AB的中点，所以OE∥PA．
因为PA?平面PAC，OE?平面PAC，
所以OE∥平面PAC．因为OM∥AC，
又AC?平面PAC，OM?平面PAC，
所以OM∥平面PAC．
因为OE?平面MOE，OM?平面MOE，OE∩OM=O，
所以平面MOE∥平面PAC．…（5分）
（2）因为点C在以AB为直径的⊙O上，
所以∠ACB=90°，即BC⊥AC．
因为PA⊥平面ABC，BC?平面ABC，
所以PA⊥BC．
因为AC?平面PAC，PA?平面PAC，PA∩AC=A，
所以BC⊥平面PAC．
因为BC?平面PBC，
所以平面PAC⊥平面PBC．…（10分）

点评 本题考查面面平行的证明，考查面面垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．