题目内容
3.参数方程$\left\{\begin{array}{l}x=cosθ\\ y=1+cosθ\end{array}\right.$(θ∈R)化为普通方程是x2+(y-1)2=1.分析 利用同角三角函数平方关系,可得结论.
解答 解:由题意,消去参数θ,可得普通方程是x2+(y-1)2=1,
故答案为x2+(y-1)2=1.
点评 本题考查参数方程化为普通方程,考查同角三角函数平方关系,比较基础.

练习册系列答案
相关题目
8.已知x、y满足曲线方程x2+$\frac{1}{{y}^{2}}$=2,则x2+y2的取值范围是( )
| A. | [0,+∞) | B. | [2,+∞) | C. | [$\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,$\frac{5}{2}$) |
12.已知复数z=$\frac{1}{1+i}$,则( )
| A. | z的实部为-$\frac{1}{2}$ | B. | z的虚部为-$\frac{1}{2}$i | ||
| C. | |z|=$\frac{1}{2}$ | D. | z的共轭复数为$\frac{1}{2}$+$\frac{1}{2}$i |
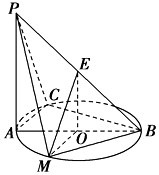 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.