题目内容
1.数列{an}的前n项和${S_n}=\frac{n}{n+1}$,数列{bn}的通项公式为bn=n-8,则bnSn的最小值为-4.分析 由等差数列通项公式求得an=n(n+1),采用“裂项法”即可求得数列的前n项和为Sn,bnSn=(n-8)(1-$\frac{1}{n+1}$)=n+1+$\frac{9}{n+1}$-10,利用基本不等式的性质,即可求得bnSn的最小值
解答 -解:由题意可知:an=2×$\frac{n(n+1)}{2}$=n(n+1),
∴$\frac{1}{{a}_{n}}$=$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
Sn=(1-$\frac{1}{2}$)+($\frac{1}{2}$-$\frac{1}{3}$)+($\frac{1}{3}$-$\frac{1}{4}$)+…+($\frac{1}{n}$-$\frac{1}{n+1}$)=1-$\frac{1}{n+1}$
则bnSn=(n-8)(1-$\frac{1}{n+1}$)=n+1+$\frac{9}{n+1}$-10≥2$\sqrt{(n+1)×\frac{9}{n+1}}$-10=-4,
当且仅当n+1=$\frac{9}{n+1}$,即n=2时取最小值-4,
∴bnSn的最小值-4,
故答案为:-4.
点评 本题考查等差数列通项公式,“裂项法”求数列的前n项和,考查数列与基本不等式相结合,考查计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知复数z=$\frac{1}{1+i}$,则( )
| A. | z的实部为-$\frac{1}{2}$ | B. | z的虚部为-$\frac{1}{2}$i | ||
| C. | |z|=$\frac{1}{2}$ | D. | z的共轭复数为$\frac{1}{2}$+$\frac{1}{2}$i |
9.某单位有职工200名,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组.若第5组抽出的号码为22,则第10组抽出的号码应是( )
| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
16.若“?x∈(0,+∞),x+$\frac{4}{x}$≥a”与“?x∈R,x2+2x+a=0”都是真命题,则a的取值范围是( )
| A. | a≤4 | B. | a≤1 | C. | 1≤a≤4 | D. | ∅ |
10.已知x0是函数f(x)=3x+$\frac{2}{1-x}$的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)<0 | D. | f(x1)>0,f(x2)>0 |
11.下列刻画一组数据离散程度的是( )
| A. | 平均数 | B. | 方差 | C. | 中位数 | D. | 众数 |
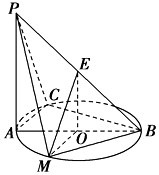 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.