题目内容

11．直线y=kx+1与圆x2+y2=1的位置关系是（　　）
A．相交B．相切C．相交或相切D．不能确定

分析 求出直线系经过的定点，判断定点与圆的位置关系即可．

解答 解：直线y=kx+1恒过（0，1），因为（0，1）在圆x2+y2=1上，所以直线y=kx+1与圆x2+y2=1的位置关系是：相交或相切．
故选：C．

点评 本题考查直线与圆的位置关系的应用，考查计算能力．

练习册系列答案
相关题目
1．椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），作直线l交椭圆于P，Q两点．M为线段PQ的中点，O为坐标原点，设直线1的斜率为k1，直线OM的斜率为k2，k1k2=-$\frac{2}{3}$．
（I）求椭圆C的离心率；
（Ⅱ）设直线l与x轴交于点D（-5，0），且满足$\overrightarrow{DP}$=2$\overrightarrow{QD}$，当△0PQ的面积最大时，求椭圆C的方程．
2．已知全集U={0，1，2，3，4，5，6}，集合A={x∈Z|x2-5x+6≤0}，集合B={1，3，4，6}，则集合A∩（∁UB）=（　　）
A．{0}B．{2}C．{0，1，2，4，6}D．{0，2，3，5}
19．已知函数$f（x）=\frac{1}{2}cos（ω\;x+\frac{π}{3}）$，且f（x+3）-f（x）=0，则ω为（　　）
A．$\frac{π}{2}$B．$\frac{2π}{3}$C．πD．$\frac{3π}{2}$
6．设数列an=min{k+$\frac{n}{4k}$|k∈N*），定义“优数列”：△an=an-[an]（n=1，2，…），其中[x]表示不超过x的最大整数．（1）求a1，a2，a3，a4的值；
（2）探究数列{an}的单调性；
（3）探究优数列：△a1，△a2，…，△a2015中等于0的项的个数；
（4）设Sn=△a1+△a2+…+△an为优数列的前n项和，试求S2015的值．
16．已知数列{an}中，a1=1，an=an-1+$\frac{1}{2}$（n≥2），则数列{an}的前9项和等于（　　）
A．27B．25C．23D．21
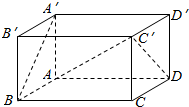3．如图，长方体ABCD-A′B′C′D′中，AD=2AB=2AA′=2．
（1）求证：A′B⊥平面ADC′；
（2）求二面角D′-AC-D的正切值．
20．已知函数$f（x）=\frac{2x+b}{{1+{x^2}}}$是定义在（m，1）上的奇函数（a，b，m为常数）．
（1）确定函数f（x）的解析式及定义域；
（2）判断并利用定义证明f（x）在（m，1）上的单调性；
（3）若对任意t∈[-2，2]，是否存在实数x使f（tx-2）+f（x）＜0恒成立？若存在，则求出实数x的取值范围，若不存在则说明理由．
1．在直角坐标系xOy中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设直线l：ρcosθ+$\sqrt{3}$ρsinθ=2$\sqrt{2}$与圆C：ρ=2交于A、B两点．
（Ⅰ）求A、B两点的极坐标；
（Ⅱ）设P是圆C上的动点，求△PAB面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网