题目内容
已知圆x2+y2-2ax-6ay+10a2-4a=0(0<a≤4)的圆心为C,直线L:y=x+m.
(1)若a=2,求直线L被圆C所截得的弦长|AB|的最大值;
(2)若m=2,求直线L被圆C所截得的弦长|AB|的最大值;
(3)若直线L是圆心C下方的切线,当a变化时,求实数m的取值范围.
(1)若a=2,求直线L被圆C所截得的弦长|AB|的最大值;
(2)若m=2,求直线L被圆C所截得的弦长|AB|的最大值;
(3)若直线L是圆心C下方的切线,当a变化时,求实数m的取值范围.
考点:直线与圆的位置关系,圆的切线方程
专题:直线与圆
分析:(1)a=2,求出圆的圆心与半径,利用直线L被圆C所截得的弦长|AB|的最大值是直径,求出直径即可;
(2)通过m=2,利用半弦长、半径、弦心距满足的勾股定理,即可利用二次函数求直线L被圆C所截得的弦长|AB|的最大值;
(3)直线L是圆心C下方的切线,利用半弦长、半径、弦心距满足的勾股定理,得到a与m的关系式,当a变化时,求实数m的取值范围.
(2)通过m=2,利用半弦长、半径、弦心距满足的勾股定理,即可利用二次函数求直线L被圆C所截得的弦长|AB|的最大值;
(3)直线L是圆心C下方的切线,利用半弦长、半径、弦心距满足的勾股定理,得到a与m的关系式,当a变化时,求实数m的取值范围.
解答:
解:圆C的方程可化为(x-a)2+(y-3a)2=4a…(1分)
∴圆心为C(a,3a),半径为r=2
…(2分)
(1)若a=2,则c(2,6),r=2
,
∵弦AB过圆心时最长,
∴|AB|max=4
…(4分)
(2)若m=2,
则圆心C(a,3a)到直线x-y+2=0的距离
d=
=
|a-1|,r=2
…(5分)
直线与圆相交,
∴d<r,∴a2-4a+1<0且0<a≤4,
∴a∈(2-
,2+
)…(6分)
又|AB|=2
=2
=2
,…(7分)
∴当a=2时,|AB|max=2
…(8分)
(3)圆心C(a,3a)到直线x-y+m=0的距离d=
…(9分)
∵直线L是圆心C的切线,
∴d=r,
=2
,|m-2a|=2
∴m=2a±2
…(11分)
∵直线L是圆心C下方,
∴m=2a-2
=(O-1)2-1…(12分)
∵a∈(0,4],
∴当a=y时,mmin=-1; 当a=4时,mmax=8-41,…(13分)
故实数m的取值范围是[-1,8-42]…(14分)
∴圆心为C(a,3a),半径为r=2
| a |
(1)若a=2,则c(2,6),r=2
| 2 |
∵弦AB过圆心时最长,
∴|AB|max=4
| 2 |
(2)若m=2,
则圆心C(a,3a)到直线x-y+2=0的距离
d=
| |-2a+2| | ||
|
| 2 |
| a |
直线与圆相交,
∴d<r,∴a2-4a+1<0且0<a≤4,
∴a∈(2-
| 3 |
| 3 |
又|AB|=2
| r2-d2 |
| -2a2+8a-2 |
| -2(a-2)2+6 |
∴当a=2时,|AB|max=2
| 6 |
(3)圆心C(a,3a)到直线x-y+m=0的距离d=
| |-2a+m| | ||
|
∵直线L是圆心C的切线,
∴d=r,
| |m-2a| | ||
|
| a |
| 2a |
∴m=2a±2
| 2a |
∵直线L是圆心C下方,
∴m=2a-2
| 2a |
∵a∈(0,4],
∴当a=y时,mmin=-1; 当a=4时,mmax=8-41,…(13分)
故实数m的取值范围是[-1,8-42]…(14分)
点评:本题考查直线与圆的位置关系,函数的最值,考查数形结合以及计算能力、转化思想的应用.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
如果直线ax+by=2与圆x2+y2=4相切,那么a+b的最大值为( )
| A、1 | ||||
B、
| ||||
| C、2 | ||||
D、
|
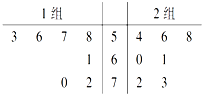 如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图.设1,2两组数据的平均数依次为
如图是1,2两组各7名同学体重(单位:kg)数据的茎叶图.设1,2两组数据的平均数依次为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
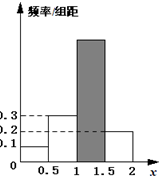 如图所示的频率分布直方图,其中阴影部分的小长方形的高度是( )
如图所示的频率分布直方图,其中阴影部分的小长方形的高度是( )| A、0.4 | B、0.8 |
| C、1.4 | D、1.6 |
一个空间几何体的三视图及其相关数据如图所示,则这个空间几何体的表面积是( )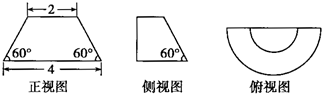

A、
| ||||
B、
| ||||
| C、11π | ||||
D、
|