题目内容
12.已知某地区一次联考中10000名学生的数学成绩服从正态分布N(120,100),则数学成绩高于130分的学生人数大约为( )附:X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.6826;P(μ-2σ<X≤μ+2σ)=0.9544;P(μ-3σ<X≤μ+3σ)=0.9974.
| A. | 3174 | B. | 1587 | C. | 456 | D. | 6828 |
分析 根据考试的成绩ξ服从正态分布N(120,100),得到考试的成绩ξ关于ξ=120对称,根据P(110≤ξ≤130)=0.6826,得到P(ξ≥120)=0.1587,根据频率乘以样本容量得到这个分数段上的人数.
解答 解:∵数学成绩服从正态分布N(120,100),∴数学成绩ξ关于ξ=120对称,
∵P(110≤ξ≤130)=0.6826,
∴P(ξ≥130)=P(ξ≤110)=$\frac{1}{2}$(1-0.6826)=0.1587,
∴该班数学成绩在130分以上的人数为0.1587×10000=1587.
故选:B.
点评 本题考查正态曲线的特点及曲线所表示的意义,是一个基础题,解题的关键是考试的成绩ξ关于ξ=120对称,利用对称写出要用的一段分数的频数,题目得解.

练习册系列答案
相关题目
2.某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取( )名学生.
| A. | 40 | B. | 50 | C. | 60 | D. | 70 |
3.若cos($\frac{π}{6}$-α)=$\frac{3}{5}$,则cos($\frac{5π}{6}$+α)的值是( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
17.集合M={x|0≤x<2},集合N={x|x2+2x-3<0},则集合M∩N=( )
| A. | {x|0≤x<1} | B. | {x|0≤x<2} | C. | {x|0≤x≤1} | D. | {x|0≤x≤2} |
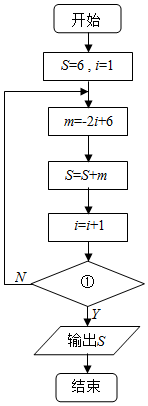 如果图中所示的流程图的输出结果为-18,那么在判断框①中用i表示的“条件”应该是i>8?.
如果图中所示的流程图的输出结果为-18,那么在判断框①中用i表示的“条件”应该是i>8?.