题目内容
7.已知复数Z=(m2+5m+6)+(m2-2m-15)i,当实数m为何值时:(1)Z为实数;
(2)Z为纯虚数;
(3)复数Z对应的点Z在第四象限.
分析 (1)由m2-2m-15=0,解出即可得出;
(2)利用纯虚数的定义,由$\left\{\begin{array}{l}{{m}^{2}+5m+6=0}\\{{m}^{2}-2m-15=0}\end{array}\right.$解出即可得出;
(3)利用复数的几何意义可得$\left\{\begin{array}{l}{{m}^{2}+5m+6>0}\\{{m}^{2}-2m-15<0}\end{array}\right.$.
解答 解:(1)由m2-2m-15=0,得m=-3或m=5.所以,当m=-3或m=5时,z为实数;
(2)由$\left\{\begin{array}{l}{{m}^{2}+5m+6=0}\\{{m}^{2}-2m-15=0}\end{array}\right.$得m=-2.所以,当m=-2时,z为纯虚数;
(3)由$\left\{\begin{array}{l}{{m}^{2}+5m+6>0}\\{{m}^{2}-2m-15<0}\end{array}\right.$得-2<m<5.
所以,当-2<m<5时,复数z对应的点Z在第四象限.
点评 本题考查了复数的有关知识、不等式的解法、几何意义,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.某同学让一弹性球从128m高处下落,每次着地后又跳回原来的高度的一半再落下,则第8次着地时球所运行的路程和为( )
| A. | 382m | B. | 510m | C. | 254m | D. | 638m |
12.已知某地区一次联考中10000名学生的数学成绩服从正态分布N(120,100),则数学成绩高于130分的学生人数大约为( )
附:X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.6826;P(μ-2σ<X≤μ+2σ)=0.9544;P(μ-3σ<X≤μ+3σ)=0.9974.
附:X~N(μ,σ2),则P(μ-σ<X≤μ+σ)=0.6826;P(μ-2σ<X≤μ+2σ)=0.9544;P(μ-3σ<X≤μ+3σ)=0.9974.
| A. | 3174 | B. | 1587 | C. | 456 | D. | 6828 |
19.过点(0,6)且与圆(x-1)2+(y-1)2=1相切的直线方程是( )
| A. | 12x-5y+30=0 | B. | 12x+5y-30=0 | ||
| C. | x=0或12x-5y+30=0 | D. | x=0或12x+5y-30=0 |
16.执行如图所示的流程图,则输出的S=( )
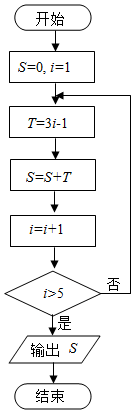

| A. | 57 | B. | 40 | C. | 26 | D. | 17 |