题目内容
已知向量
=（2，-3），
=（-5，4），
=（1-λ，3λ+2）．
（Ⅰ）若△ABC为直角三角形，且∠B为直角，求实数λ的值；
（Ⅱ）若点A、B、C能构成三角形，求实数λ应满足的条件．
| OA |
| OB |
| OC |
（Ⅰ）若△ABC为直角三角形，且∠B为直角，求实数λ的值；
（Ⅱ）若点A、B、C能构成三角形，求实数λ应满足的条件．
考点：向量在几何中的应用
专题：平面向量及应用
分析：（Ⅰ）由∠B是直角，得BA⊥BC，即
•
=0，据此可列出关于λ的方程，解之即可；
（Ⅱ）若三点是三角形的三个顶点，则只需三点A、B、C不共线即可，求出共线时λ的范围，然后取其补集就是所求．
| BA |
| BC |
（Ⅱ）若三点是三角形的三个顶点，则只需三点A、B、C不共线即可，求出共线时λ的范围，然后取其补集就是所求．
解答：
解：（Ⅰ）因为△ABC是直角三角形，且∠B=90°，
所以
•
=0，又因为
=（2，-3），
=（-5，4），
=（1-λ，3λ+2），
∴（
-
）•（
-
）=（7，-7）•（6-λ，3λ-2）=0
即8-4λ=0，解得λ=2．
（Ⅱ）若点A、B、C能构成三角形，则A、B、C不共线，
∴向量
与
不共线，即-7（3λ-2）≠7（6-λ），
∴实数λ应满足条件λ≠-2．
所以
| BA |
| BC |
| OA |
| OB |
| OC |
∴（
| OA |
| OB |
| OC |
| OB |
即8-4λ=0，解得λ=2．
（Ⅱ）若点A、B、C能构成三角形，则A、B、C不共线，
∴向量
| BA |
| BC |
∴实数λ应满足条件λ≠-2．
点评：这是一道向量在研究几何位置关系中的应用，主要考查了利用数量积证垂直，利用向量共线证平行的思路，计算一定要准确．
练习册系列答案
名校课堂系列答案
相关题目
已知向量
=（1，1），
=（2，x），若
+
∥4
-2
，则实数x的值是（ ）
| a |
| b |
| a |
| b |
| b |
| a |
| A、-2 | B、0 | C、1 | D、2 |
方程x3-（
）x-2=0的根所在的区间为（ ）
| 1 |
| 2 |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
如果复数z1=a+6i，z2=3-4i，且
为纯虚数，那么实数a的值为（ ）
| z1 |
| z2 |
A、-
| ||
| B、0 | ||
| C、2 | ||
| D、8 |
已知（
）m＜（
）n＜1，则有（ ）
| 1 |
| 2 |
| 1 |
| 2 |
| A、0＜n＜m |
| B、n＜m＜0 |
| C、0＜m＜n |
| D、m＜n＜0 |
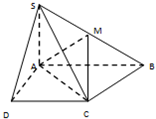如图已知四棱锥S-ABCD的底面是直角梯形，AB∥DC，∠DAB=90°，SA⊥底面ABCD，且SA=AD=DC=