题目内容
13.在△ABC中,角A、B、C所对的边分别为a、b、c,如果$\frac{a}{b}$=2$\sqrt{3}$cos(B+C),B=30°,那么角A等于( )| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
分析 使用正弦定理化简$\frac{a}{b}$=2$\sqrt{3}$cos(B+C)得出tanA.
解答 解:在△ABC中,由正弦定理得$\frac{a}{b}=\frac{sinA}{sinB}=-2\sqrt{3}cosA$,
∴tanA=$\frac{sinA}{cosA}$=-2$\sqrt{3}$sinB=-$\sqrt{3}$.
∴A=120°.
故选:C.
点评 本题考查了正弦定理的应用,属于基础题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
4.已知tan(α-$\frac{π}{4}$)=$\frac{1}{2}$,则$\frac{sinα+cosα}{sinα-cosα}$的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | -2 |
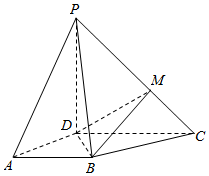 如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=2,CD=3,M为PC上一点,PM=2MC.
如图,四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,∠BAD=$\frac{π}{3}$,AB=2,CD=3,M为PC上一点,PM=2MC.