题目内容
5.设函数f(x)在点x=a处可导,试用a、f(a)和f′(a)表示$\underset{lim}{x→a}$$\frac{af(x)-xf(a)}{x-a}$.分析 利用导数的概念变形得出$\underset{lim}{x→a}$$\frac{af(x)-af(a)+af(a)-xf(a)}{x-a}$=$\underset{lim}{x→a}$[a$\frac{f(x)-f(a)}{x-a}$-f(a)],根据极限式子可判断为af′(a)-f(a).
解答 解:∵$\underset{lim}{x→a}$$\frac{af(x)-xf(a)}{x-a}$=$\underset{lim}{x→a}$$\frac{af(x)-af(a)+af(a)-xf(a)}{x-a}$=$\underset{lim}{x→a}$[a$\frac{f(x)-f(a)}{x-a}$-f(a)]=a$\underset{lim}{x→a}$$\frac{f(x)-f(a)}{x-a}$-f(a)=af′(a)-f(a).
∴$\underset{lim}{x→a}$$\frac{af(x)-xf(a)}{x-a}$=af′(a)-f(a).
点评 本题考查了导数的概念,性质,运用,关键是恒等变形得出需要的式子,可判断出答案.

练习册系列答案
相关题目
13.在△ABC中,角A、B、C所对的边分别为a、b、c,如果$\frac{a}{b}$=2$\sqrt{3}$cos(B+C),B=30°,那么角A等于( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
20.若2cos2α=sin($\frac{π}{4}$-α),且α∈($\frac{π}{2}$,π),则sin2α的值为( )
| A. | -$\frac{7}{8}$ | B. | -$\frac{\sqrt{15}}{8}$ | C. | 1 | D. | $\frac{\sqrt{15}}{8}$ |
14.已知椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点分别是F1,F2,短轴一个端点M(0,b),直线l:4x+3y=0交椭圆E于A,B两点,若|AF1|+|BF1|=6,点M到直线l的距离不小于$\frac{6}{5}$,则椭圆E的离心率范围是( )
| A. | $(0,\frac{{\sqrt{5}}}{3}]$ | B. | $[\frac{{\sqrt{5}}}{3},1)$ | C. | $(0,\frac{{\sqrt{3}}}{2}]$ | D. | $[\frac{{\sqrt{3}}}{2},1)$ |
15.若实数x,y满足$\left\{\begin{array}{l}x+y-1≤0\\ 2x-y-2≤0\\ y≤1.\end{array}\right.$,则目标函数z=x-3y的最小值为( )
| A. | 0 | B. | 1 | C. | $-\frac{3}{2}$ | D. | -3 |
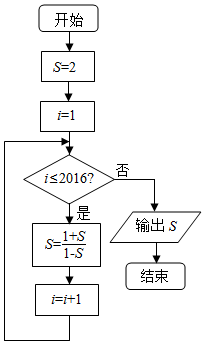
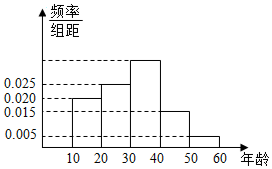 随机抽取100名年龄在[10,20),[20,30)…,[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人,则在[50,60)年龄段抽取的人数为2.
随机抽取100名年龄在[10,20),[20,30)…,[50,60)年龄段的市民进行问卷调查,由此得到样本的频率分布直方图如图所示,从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人,则在[50,60)年龄段抽取的人数为2.