题目内容
若函数y=x2-4x-4的定义域为[0,m],值域为[-8,-4],则m的取值范围是( )
| A、(2,4) |
| B、[2,4) |
| C、(2,4] |
| D、[2,4] |
考点:二次函数的性质,函数的定义域及其求法
专题:函数的性质及应用
分析:根据二次函数y=x2-4x-4的图象与性质,结合x∈[0,m],函数y的值域,求出m的取值范围.
解答:
解:∵函数y=x2-4x-4=(x-2)2-8,
∴函数y的对称轴是x=2,
且x=2时,y取得最小值-8,
x=0或4时,y=-4;
又∵当x∈[0,m],函数y的值域为[-8,-4],
∴2≤m≤4;
∴m的取值范围是[2,4].
故选:D.
∴函数y的对称轴是x=2,
且x=2时,y取得最小值-8,
x=0或4时,y=-4;
又∵当x∈[0,m],函数y的值域为[-8,-4],
∴2≤m≤4;
∴m的取值范围是[2,4].
故选:D.
点评:本题考查了二次函数的图象与性质的应用问题,也考查了函数的定义域和值域的应用问题,是基础题目.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
设两个向量
=(n+2,n-cos2x),
=(m,
+sinx),其中m,n为实数,若存在实数x使得
=2
,则m的取值范围为( )
| a |
| b |
| m |
| 2 |
| a |
| b |
| A、[1,4] |
| B、[0,4] |
| C、[0,2] |
| D、[-6,-2] |
已知i是虚数单位,复数z=
,则|z-2|=( )
| 2i |
| 1+i |
| A、2 | ||
B、2
| ||
C、
| ||
| D、1 |
若非零实数a,b,c成等差数列,则函数y=ax2+bx+
c的图象与x轴交点的个数为( )
| 1 |
| 4 |
| A、0 | B、1 | C、2 | D、1或2 |
函数y=x2-4ax+1在区间[-2,4]上单调递增函数,则实数a的取值范围是( )
| A、(-∞,2] |
| B、(-∞,-1] |
| C、[2,+∞) |
| D、[-1,+∞) |
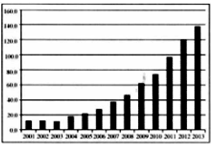 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A、y=ax2+bx+c |
| B、y=aex+b |
| C、y=eax+b |
| D、y=alnx+b |
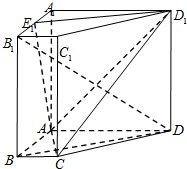 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.