题目内容
某班组织文艺晚会,准备从A,B等8个节目中选出4个节目演出,要求:A,B两个节目至少有一个选中,且A,B同时选中时,它们的演出顺序不能相邻,那么不同演出顺序的和数为( )
| A、1860 | B、1320 |
| C、1140 | D、1020 |
考点:排列、组合及简单计数问题
专题:应用题,排列组合
分析:分两类:第一类,A,B只有一个选中,第二类:A,B同时选中,利用加法原理即可得出结论.
解答:
解:分两类:第一类,A,B只有一个选中,则不同演出顺序有
种;
第二类:A,B同时选中,则不同演出顺序有
种.
共有:
+
=1140(种).
故选:C.
| C | 1 2 |
| C | 3 6 |
| A | 4 4 |
第二类:A,B同时选中,则不同演出顺序有
| C | 2 6 |
| A | 2 2 |
| A | 2 3 |
共有:
| C | 1 2 |
| C | 3 6 |
| A | 4 4 |
| C | 2 6 |
| A | 2 2 |
| A | 2 3 |
故选:C.
点评:本题考查排列、组合的实际应用,正确分类是关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
函数y=x2-4ax+1在区间[-2,4]上单调递增函数,则实数a的取值范围是( )
| A、(-∞,2] |
| B、(-∞,-1] |
| C、[2,+∞) |
| D、[-1,+∞) |
已知{an}中,a1=1,
=
,则数列{an}的通项公式是( )
| an+1 |
| an |
| 1 |
| 2 |
| A、an=2n | ||
B、an=
| ||
C、an=
| ||
D、an=
|
 正三棱柱ABC-A1B1C1中,点D是BC的中点,BC=2,BB1=
正三棱柱ABC-A1B1C1中,点D是BC的中点,BC=2,BB1=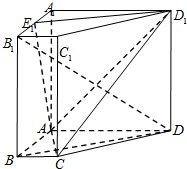 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点. 如图,已知椭圆C:
如图,已知椭圆C: