题目内容
 已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<
已知两个电流瞬时值的函数表达式分别为 I1(t)=sint,I2(t)=sin(t+φ),|φ|<| π |
| 2 |
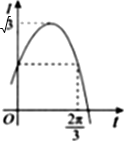
考点:y=Asin(ωx+φ)中参数的物理意义
专题:三角函数的图像与性质
分析:利用三角函数的和差化积公式将函数进行化简,结合三角函数的最大值和对称性进行求解即可.
解答:
解:I(t)=I1(t)+I2(t)=sint+sin(t+φ)=2sin
cos
=2sin(t+
)cos
,
由图象知函数的最大值为
,
即2cos
=
,
即cos
=
,
即
=±
,则φ=±
,
∵函数的对称轴为x=
=
,为此时函数取得最大值,
∴
+
=
,
即
=
-
=
,
∴φ=
,
则I(t)=
sin(t+
),
故答案为:
sin(t+
),
.
| t+t+φ |
| 2 |
| t-t-φ |
| 2 |
| φ |
| 2 |
| φ |
| 2 |
由图象知函数的最大值为
| 3 |
即2cos
| φ |
| 2 |
| 3 |
即cos
| φ |
| 2 |
| ||
| 2 |
即
| φ |
| 2 |
| π |
| 6 |
| π |
| 3 |
∵函数的对称轴为x=
| ||
| 2 |
| π |
| 3 |
∴
| π |
| 3 |
| φ |
| 2 |
| π |
| 2 |
即
| φ |
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴φ=
| π |
| 3 |
则I(t)=
| 3 |
| π |
| 6 |
故答案为:
| 3 |
| π |
| 6 |
| π |
| 3 |
点评:本题主要考查三角函数的解析式的求解,根据三角函数的图象结合三角函数的和差化积公式是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
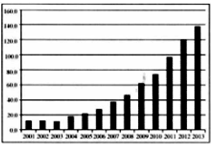 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A、y=ax2+bx+c |
| B、y=aex+b |
| C、y=eax+b |
| D、y=alnx+b |
已知{an}中,a1=1,
=
,则数列{an}的通项公式是( )
| an+1 |
| an |
| 1 |
| 2 |
| A、an=2n | ||
B、an=
| ||
C、an=
| ||
D、an=
|
已知凼数F(x)为二次凼数,且F(x)的导凼数为f(x),若存在实数a∈(-2,-1),使f(-a)=-f(a)>0,则不等式F(2x-1)>F(x)的解集为( )
A、{x|x<
| ||
B、{x|x<
| ||
C、{x|
| ||
D、{x|x<-1或x>-
|
已知直线ax+by=0与双曲线
-
=1(0<a<b)交于A,B两点,若A(x1,y1),B(x2,y2)满足|x1-x2|=3
,且|AB|=6,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
| B、3 | ||
C、
| ||
| D、2 |
已知
、
的夹角为120°,且|
|=1,|2
+
|=2
,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| 3 |
| b |
A、3
| ||
B、2
| ||
| C、4 | ||
| D、2 |
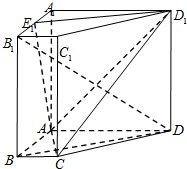 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面 ABCD,底面ABCD是直角梯形,AD∥BC,∠BAD=90°,AD=AA1=3,BC=1,E1为A1B1中点.