题目内容
6.某赛季甲乙两名篮球运动员每场比赛得分的原始记录如下:甲运动员得分:30,27,9,14,33,25,21,12,36,23,
乙运动员得分:49,24,12,31,50,31,44,36,15,37,25,36,39
(1)根据两组数据完成甲乙运动员得分的茎叶图,并通过茎叶图比较两名运动员成绩的平均值及稳定程度;(不要求计算出具体数值,给出结论即可)
(2)若从甲运动员的十次比赛的得分中选出2个得分,记选出的得分超过23分的个数为ξ,求ξ的分布列和数学期望.
分析 (Ⅰ)由某赛季甲乙两名篮球运动员每场比赛得分的原始记录作出茎叶图,由茎叶图得,乙的平均值大于甲的平均数,甲比乙稳定.
(Ⅱ)根据题意ξ的所有可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和数学期望.
解答 (12分)
解:(Ⅰ)由某赛季甲乙两名篮球运动员每场比赛得分的原始记录作出茎叶图: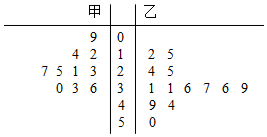
由茎叶图得,乙的平均值大于甲的平均数,甲比乙稳定.…(6分)
(Ⅱ)根据题意ξ的所有可能取值为0,1,2,
则$P({ξ=0})=\frac{C_5^2}{{C_{10}^2}}=\frac{2}{9}$,
$P({ξ=1})=\frac{C_5^1C_5^1}{{C_{10}^2}}=\frac{5}{9}$,
$P({ξ=2})=\frac{C_5^2}{{C_{10}^2}}=\frac{2}{9}$,
所以ξ的分布列为
| ξ | 0 | 1 | 2 |
| P(ξ) | $\frac{2}{9}$ | $\frac{5}{9}$ | $\frac{2}{9}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
17.双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)的右焦点为F(c,0),若圆C:(x-c)2+y2=4a2与双曲线E的渐近线相切,则E的离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{3}+1}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
14.过点E(1,0)作两条互相垂直的直线交抛物线y2=4x于点A、B、C、D,且M、N分别是AB、CD的中点,则三角形EMN面积的最小值为( )
| A. | 2 | B. | 3 | C. | $\frac{1}{3}$ | D. | 4 |
16.对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(单位:m/s)的数据如表:
(1)画出茎叶图;
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、方差,你认为选谁参加比赛更合适并说明理由.
| 甲 | 29 | 37 | 35 | 33 | 26 | 50 |
| 乙 | 32 | 33 | 28 | 34 | 40 | 43 |
(2)分别求出甲、乙两名自行车赛手最大速度(单位:m/s)的数据的平均数、方差,你认为选谁参加比赛更合适并说明理由.