题目内容
已知直线l1为曲线y=x2+x-2在点(0,-2)处的切线,l2为该曲线的另一条切线,且l1⊥l2
(Ⅰ)求直线l2的方程;
(Ⅱ)求由直线l1、l2和x轴所围成的三角形的面积.
(Ⅰ)求直线l2的方程;
(Ⅱ)求由直线l1、l2和x轴所围成的三角形的面积.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)根据导数的几何意义以及直线垂直的关系即可求直线l2的方程;
(Ⅱ)根据三角形的面积公式即可求由直线l1、l2和x轴所围成的三角形的面积.
(Ⅱ)根据三角形的面积公式即可求由直线l1、l2和x轴所围成的三角形的面积.
解答:
解:(Ⅰ)函数的导数为f′(x)=2x+1,
则在点(0,-2)处的切线斜率k=f′(0)=1,
∴l1:x-y-2=0,
∵l1⊥l2,
∴直线l2的斜率k=-1;
由f′(x)=2x+1=-1,即2x=-2,
解得x=-1,此时y=-2,直线l2的切点为(-1,-2),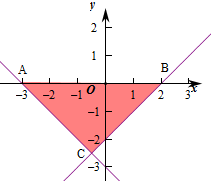
则直线l2的方程为y+2=-(x+1),即x+y+3=0.
(Ⅱ)∵l1:x-y-2=0,l2:x+y+3=0,
∴
,解得
,
即C(-
,-
),
又A(-3,0),B(2,0),
则由直线l1、l2和x轴所围成的三角形的面积S=
×5×
=
.
则在点(0,-2)处的切线斜率k=f′(0)=1,
∴l1:x-y-2=0,
∵l1⊥l2,
∴直线l2的斜率k=-1;
由f′(x)=2x+1=-1,即2x=-2,
解得x=-1,此时y=-2,直线l2的切点为(-1,-2),

则直线l2的方程为y+2=-(x+1),即x+y+3=0.
(Ⅱ)∵l1:x-y-2=0,l2:x+y+3=0,
∴
|
|
即C(-
| 1 |
| 2 |
| 5 |
| 2 |
又A(-3,0),B(2,0),
则由直线l1、l2和x轴所围成的三角形的面积S=
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 4 |
点评:本题主要考查函数切线的求解以及直线垂直的关系,利用导数的几何意义是解决本题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
设
=2,则tan(α+
)=( )
| sinα+cosα |
| sinα-cosα |
| π |
| 4 |
| A、-2 | B、2 | C、-4 | D、4 |
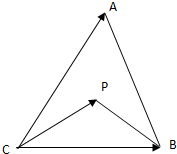 如图示,已知A、B、C为平面上的三个定点,∠ACB=60°,动点P在∠ACB的平分线上,记
如图示,已知A、B、C为平面上的三个定点,∠ACB=60°,动点P在∠ACB的平分线上,记