题目内容
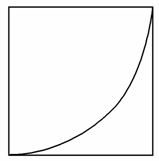
如图,已知AB为圆O的直径,BC切圆O于点B,AC交圆O于点P,E为线段BC的中点.求证:OP⊥PE.

因为AB是圆O的直径,
所以∠APB=90°,从而∠BPC=90°.
在△BPC中,因为E是边BC的中点,所以BE=EC,从
而BE=EP,因此∠1=∠3.
又因为B、P为圆O上的点,所以OB=OP,从而∠2=∠4.
因为BC切圆O于点B,所以∠ABC=90°,即∠1+∠2=90°,
从而∠3+∠4=90°,于是∠OPE=90°.
所以OP⊥PE.

练习册系列答案
相关题目
 中,已知椭圆
中,已知椭圆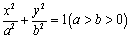 与直线
与直线 相交于
相交于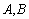 两点(从左至右),过点
两点(从左至右),过点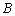 作
作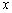 轴的垂线,垂足为
轴的垂线,垂足为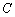 ,直线
,直线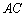 交椭圆于另一点
交椭圆于另一点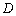 .
.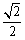 ,点
,点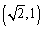 ,求椭圆的方程;
,求椭圆的方程;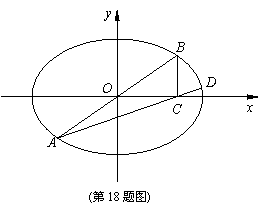 (2)若以
(2)若以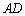 为直径的圆恰好经过点
为直径的圆恰好经过点 中,
中, ,且
,且 分别是
分别是 的中点.
的中点. 求证:(1)直线EF ∥面ACD ;
求证:(1)直线EF ∥面ACD ; ,那么抛物线C的方程为( )
,那么抛物线C的方程为( ) B.
B.  C.
C.  D.
D. 
 .
. 时,求不等式
时,求不等式 的解集;
的解集; 与函数
与函数 的图象恒有公共点,求实数
的图象恒有公共点,求实数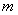 的取值范围.
的取值范围.