题目内容
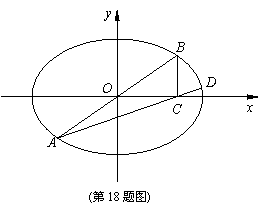
在平面直角坐标系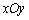 中,已知椭圆
中,已知椭圆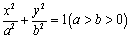 与直线
与直线 相交于
相交于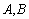 两点(从左至右),过点
两点(从左至右),过点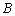 作
作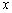 轴的垂线,垂足为
轴的垂线,垂足为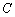 ,直线
,直线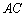 交椭圆于另一点
交椭圆于另一点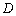 .
.
(1)若椭圆的离心率为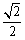 ,点
,点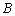 的坐标为
的坐标为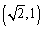 ,求椭圆的方程;
,求椭圆的方程;
 (2)若以
(2)若以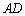 为直径的圆恰好经过点
为直径的圆恰好经过点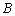 ,求椭圆的离心率.
,求椭圆的离心率.
(1)由题意, ,解得
,解得 ,所以椭圆的方程为
,所以椭圆的方程为 .
.
(2)方法一:设 ,则
,则 ,
, .
.
因为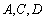 三点共线,所以
三点共线,所以 ,
,
由 ,
,
得 ,即
,即 .
.
又 均在椭圆上,
均在椭圆上,
有 ,
,
①—②,得 ,
,
所以直线 的斜率
的斜率 ,
,
由于以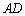 为直径的圆恰好经过点
为直径的圆恰好经过点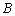 ,
,
所以 ,即
,即 ,所以
,所以 ,
,
所以椭圆的离心率 .
.
方法二:设 ,则
,则 ,
,
所以直线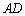 的方程为
的方程为 .
.
由 ,消
,消 ,得
,得 ,
,
即 ,
,
所以 ,
,
从而 ,即
,即 ,
,
所以直线 的斜率
的斜率 ,
,
由于以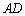 为直径的圆恰好经过点
为直径的圆恰好经过点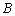 ,
,
所以 ,即
,即 ,所以
,所以 ,
,
所以椭圆的离心率 .
.

练习册系列答案
相关题目
 中,角
中,角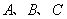 的对边分别为
的对边分别为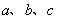 ,已知
,已知 ,
, 的值;
的值; ,求
,求 的值.
的值. 为边,
为边, 为对角线的矩形中,
为对角线的矩形中, ,
, ,则实数
,则实数 .
. ,则
,则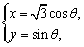 其中
其中 为参数.以
为参数.以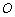 为
为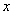 轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
轴正半轴为极轴建立极坐标系,直线l的极坐标方程为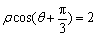 .求
.求 的一个焦点为(5,0),则实数m = .
的一个焦点为(5,0),则实数m = .
 满足
满足 其中
其中 是自然对数的底数 , 则
是自然对数的底数 , 则
 的最小值为
的最小值为