题目内容
设P1,P2,…,Pj为集合P={1,2,…,i}的子集,其中i,j为正整数.记aij为满足P1∩P2∩…∩Pj=的有序子集组(P1,P2,…,Pj)的个数.
(1)求a22的值;
(2)求aij的表达式.
1)由题意得P1,P2为集合P={1,2}的子集,
因为P1∩P2=,
所以集合P={1,2}中的元素“1”共有如下3种情形:
1P1,且1 P2;1P1,且1 P2;1P1,且1P2;
同理可得集合P={1,2}中的元素“2”也有3种情形,
根据分步乘法原理得,a22=3×3=9;
(2)考虑P={1,2,…,i}中的元素“1”,有如下情形:
1不属于P1,P2,…,Pj中的任何一个,共C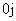 种;
种;
1只属于P1,P2,…,Pj中的某一个,共C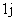 种;
种;
1只属于P1,P2,…,Pj中的某两个,共C 种;
种;
……
1只属于P1,P2,…,Pj中的某(j-1)个,共C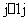 种,
种,
根据分类加法原理得,元素“1”共有C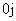 +C
+C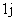 +C
+C +…+C
+…+C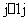 =2
=2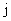 -1种情形,
-1种情形,
同理可得,集合P={1,2,…,i}中其它任一元素均有(2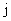 -1)种情形,
-1)种情形,
根据分步乘法原理得,aij=(2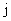 -1)i.
-1)i.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 是定义域为
是定义域为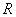 的奇函数,对于任意的
的奇函数,对于任意的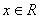
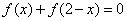 ,则函数
,则函数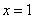 对称;
对称;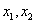 是函数
是函数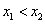 时,
时,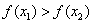 ,则
,则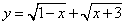 的最大值和最小值分别为
的最大值和最小值分别为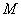 和
和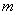 ,则
,则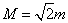 ;
;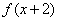 也为奇函数,则
也为奇函数,则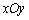 中,椭圆
中,椭圆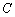 的参数方程为
的参数方程为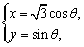 其中
其中 为参数.以
为参数.以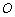 为
为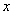 轴正半轴为极轴建立极坐标系,直线l的极坐标方程为
轴正半轴为极轴建立极坐标系,直线l的极坐标方程为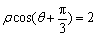 .求
.求 恒成立,则实数a的取值范围是 .
恒成立,则实数a的取值范围是 .
 上的奇函数
上的奇函数 满足
满足 ,当
,当 时,
时, ,则
,则 内是( )
内是( ) B.减函数且
B.减函数且 C.增函数且
C.增函数且
 B.
B. 




 ,其中
,其中 ,则
,则 ( )
( ) (B)
(B) (C)
(C) (D)
(D)