题目内容

16．在平面内的动点（x，y）满足不等式$\left\{\begin{array}{l}x+y-3≤0\\ x-y+1≤0\end{array}\right.$，则z=2x+y的最大值是（　　）
A．-4B．4C．-2D．2

分析 画出约束条件的可行域，利用目标函数的几何意义求解最大值即可．

解答 解：不等式组所表示的平面区域位于
直线x+y-3=0的下方区域和直线
x-y+1=0的上方区域，
根据目标函数的几何意义，
可知目标函数经过A时，z取得最大值．
由$\left\{\begin{array}{l}{x+y-3=0}\\{x-y+1=0}\end{array}\right.$可得A（1，2），
所以目标函数z的最大值为4．
故选B．

点评 本题主要考查线性规划问题．画出可行域判断目标函数的几何意义是解题的关键．

练习册系列答案
相关题目
6．设函数f（x）是R上的奇函数，f（x+π）=-f（x），当0≤x≤$\frac{π}{2}$时，f（x）=cosx-1，则-2π≤x≤2π时，f（x）的图象与x轴所围成图形的面积为（　　）
A．4π-8B．2π-4C．π-2D．3π-6
7．已知函数f（x）=aln（x+1）-x2，若对?p，q∈（0，1），且p≠q，有$\frac{{f（{p+1}）-f（{q+1}）}}{p-q}＞2$恒成立，则实数a的取值范围为（　　）
A．（-∞，18）B．（-∞，18]C．[18，+∞）D．（18，+∞）
4．二项式${（x-\frac{1}{{\root{3}{x}}}）^8}$的展开式中，常数项是28．
11．已知函数f（x）=ln（x+1）+ax，其中a∈R．
（Ⅰ） 当a=-1时，求证：f（x）≤0；
（Ⅱ） 对任意x2≥ex1＞0，存在x∈（-1，+∞），使$\frac{{f（{x_2}-1）-f（{x_1}-1）}}{{{x_2}-{x_1}}}＞\frac{{a（{x_2}-1）-f（x）}}{x_2}$成立，求a的取值范围．（其中e是自然对数的底数，e=2.71828…）
1．直线kx-3y+3=0与圆（x-1）2+（y-3）2=10相交所得弦长的最小值为2$\sqrt{5}$．
8．某几何体的三视图如图所示，则其体积为（　　）
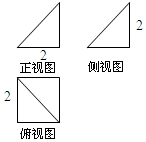
A．4B．$\frac{7}{3}$C．$\frac{4}{3}$D．$\frac{8}{3}$
5．已知等差数列{an}满足a1+a2=6，a2+a3=10．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求数列{an+an+1}的前n项和．
13．已知向量$\overrightarrow{a}$=（m，3），$\overrightarrow{b}$=（1，2），且$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$•$\overrightarrow{b}$的值为7.5．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网