题目内容
已知直线y=ax+1与双曲线3x2-y2=1交于A、B点.
(1)求a的取值范围;
(2)若以AB为直径的圆过坐标原点,求实数a的值;
(3)是否存在这样的实数a,使A、B两点关于直线y=
x对称?若存在,请求出a的值;若不存在,说明理由.
(1)求a的取值范围;
(2)若以AB为直径的圆过坐标原点,求实数a的值;
(3)是否存在这样的实数a,使A、B两点关于直线y=
| 1 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)将y=ax+1代入方程3x2-y2=1,得(a2-3)x2+2ax+2=0,由题意知a2-3≠0,且△=4a2+8(3-a2)>0,由此能求出a的取值范围.
(2)设交点为A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
,y1y2=(ax1+1)(ax2+1)=a2•x1x2+a(x1+x2)+1=1,由已知得OA⊥OB,由此求出a=±1.
(3)若A、B两点关于直线y=
x对称,则直线y=
x垂直AB,且AO=BO,由此能推导出存在实数a,使A、B两点关于直线y=
x对称.
(2)设交点为A(x1,y1),B(x2,y2),则x1+x2=-
| 2a |
| a2-3 |
| 2 |
| a2-3 |
(3)若A、B两点关于直线y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)将y=ax+1代入方程3x2-y2=1,得
3x2-(ax+1)2=1,整理,
(a2-3)x2+2ax+2=0,
∵直线y=ax+1与双曲线3x2-y2=1交于A、B点,
∴a2-3≠0,且△=4a2+8(3-a2)>0,得:a2<6,且a≠±
,
∴a的取值范围是{a||-
<a<
,且a≠±
}.
(2)设交点为A(x1,y1),B(x2,y2),
则x1+x2=-
,x1x2=
,
∴y1y2=(ax1+1)(ax2+1)=a2•x1x2+a(x1+x2)+1=1
∵以AB为直径的圆过坐标原点∴OA⊥OB,
故OA与OB的斜率的乘积为-1.
∴x1x2=-y1y2,即
=-1,
解得a=±1.
(3)若A、B两点关于直线y=
x对称,
则直线y=
x垂直AB,且AO=BO,
由直线y=
x垂直AB得出a=-2,
∴x1x2=2,x1+x2=4,
y1y2=1,y1+y2=-6,
∴AB中点为(2,-3),且不在y=
x上,
所以a=-2不成立,
综上:不存在实数a,使A、B两点关于直线y=
x对称.
3x2-(ax+1)2=1,整理,
(a2-3)x2+2ax+2=0,
∵直线y=ax+1与双曲线3x2-y2=1交于A、B点,
∴a2-3≠0,且△=4a2+8(3-a2)>0,得:a2<6,且a≠±
| 3 |
∴a的取值范围是{a||-
| 6 |
| 6 |
| 3 |
(2)设交点为A(x1,y1),B(x2,y2),
则x1+x2=-
| 2a |
| a2-3 |
| 2 |
| a2-3 |
∴y1y2=(ax1+1)(ax2+1)=a2•x1x2+a(x1+x2)+1=1
∵以AB为直径的圆过坐标原点∴OA⊥OB,
故OA与OB的斜率的乘积为-1.
∴x1x2=-y1y2,即
| 2 |
| a2-3 |
解得a=±1.
(3)若A、B两点关于直线y=
| 1 |
| 2 |
则直线y=
| 1 |
| 2 |
由直线y=
| 1 |
| 2 |
∴x1x2=2,x1+x2=4,
y1y2=1,y1+y2=-6,
∴AB中点为(2,-3),且不在y=
| 1 |
| 2 |
所以a=-2不成立,
综上:不存在实数a,使A、B两点关于直线y=
| 1 |
| 2 |
点评:本题考查实数的取值范围的求法,考查实数值的求法,考查满足条件的实数是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
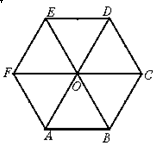 如图,设O是正六边形ABCDEF的中心,在向量
如图,设O是正六边形ABCDEF的中心,在向量| OB |
| OC |
| OD |
| OE |
| OF |
| AB |
| BC |
| CD |
| EF |
| DE |
| FA |
| OA |
| A、1个 | B、2个 | C、3个 | D、4个 |
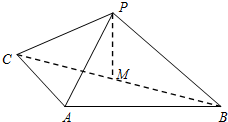 如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.
如图,△PAB是边长为2的正三角形,平面PAB外一动点C满足下面条件:PC=PA,AC⊥AB.