题目内容
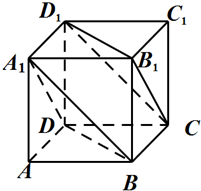如图，在正方体ABCD-A1B1C1D1中．（1）求证：平面A1BD∥平面CD1B1．
（2）求异面直线A1D与D1C所成的角．
考点：异面直线及其所成的角,平面与平面平行的判定
专题：空间位置关系与距离,空间角
分析：（1）通过平移先作出异面直线所成的角，进而求出即可；
（2）利用线面、面面平行的判定定理即可证明．
（2）利用线面、面面平行的判定定理即可证明．
解答：
（1）证明：∵几何体是正方体，∴CD∥A1B1并且CD=A1B1
∴A1D∥B1C，而A1D?平面B1CD1，B1C?平面B1CD1，
∴A1D∥平面B1CD1，
同理可得A1B∥平面CB1D1，
又∵A1D∩A1B=A1，
∴平面A1BD∥平面CB1D1．
解：（2）由（1）可知对角面A1B1CD是一个平行四边形，
∴B1C∥A1D．
∴∠B1CD1或其补角即为异面直线A1D与 D1C所成的角，
∵△B1CD1是一个等边三角形，
∴∠B1CD1=60°即为异面直线A1D与 D1C所成的角；
∴A1D∥B1C，而A1D?平面B1CD1，B1C?平面B1CD1，
∴A1D∥平面B1CD1，
同理可得A1B∥平面CB1D1，
又∵A1D∩A1B=A1，
∴平面A1BD∥平面CB1D1．
解：（2）由（1）可知对角面A1B1CD是一个平行四边形，
∴B1C∥A1D．
∴∠B1CD1或其补角即为异面直线A1D与 D1C所成的角，
∵△B1CD1是一个等边三角形，
∴∠B1CD1=60°即为异面直线A1D与 D1C所成的角；
点评：熟练掌握线面、面面平行的判定定理和性质定理、异面直线所成的角转化为平面角是解题的关键．
练习册系列答案
相关题目
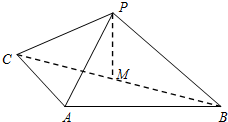如图，△PAB是边长为2的正三角形，平面PAB外一动点C满足下面条件：PC=PA，AC⊥AB．
