题目内容
已知直线a∥平面α，直线b⊥平面α，求证：a⊥b．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：设β为过a的平面，且α∩β=l．由a∥α，得a∥l．由b⊥l，得b⊥a．
解答：
证明：设β为过a的平面，且α∩β=l．
∵a∥α，∴a∥l．
∵直线b⊥平面α，l?α，
∴b⊥l，
∴b⊥a．
故a⊥b．
∵a∥α，∴a∥l．
∵直线b⊥平面α，l?α，
∴b⊥l，
∴b⊥a．
故a⊥b．
点评：本题考查直线与直线垂直的证明，是基础题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
设函数y1=ln（1-x）定义域为A，函数y2=ex-1的值域为B，则A∩B是（ ）
| A、∅ | B、R |
| C、（0，1） | D、（-1，1） |
如图所示，设F是抛物线E：x2=2py（p＞0）的焦点，过点F作斜率分别为k1、k2的两条直线l1、l2，且k1•k2=-1，l1与E相交于点A、B，l2与E相交于点C，D．已知△AFO外接圆的圆心到抛物线的准线的距离为3（O为坐标原点）．
如图所示．△ABC中，∠B=90°，M为AB上一点，使得AM=BC，N为BC上一点，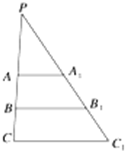
棱台的上底面积为16，下底面积为64，求棱台被它的中截面分成的上、下两部分体积之比．