题目内容
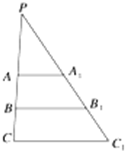 棱台的上底面积为16,下底面积为64,求棱台被它的中截面分成的上、下两部分体积之比.
棱台的上底面积为16,下底面积为64,求棱台被它的中截面分成的上、下两部分体积之比.考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:将棱台还原成棱锥,AA1、BB1、CC1分别是轴截面与小锥、中锥、大锥底面的交线,求出AA1:BB1:CC1=1:
:2=2:3:4,即可求棱台被它的中截面分成的上、下两部分体积之比.
| 3 |
| 2 |
解答:
解:将棱台还原成棱锥,AA1、BB1、CC1分别是轴截面与小锥、中锥、大锥底面的交线,
则AA1:CC1=
:
=1:2.
∵BB1为棱台轴截面的中位线,∴AA1:BB1:CC1=1:
:2=2:3:4.
∴V小:V中:V大=23:33:43=8:27:64,
∴(V中-V小):(V大-V中)=(27-8):(64-27)=19:37,
即上、下两部分体积之比为19:37.
则AA1:CC1=
| 16 |
| 64 |
∵BB1为棱台轴截面的中位线,∴AA1:BB1:CC1=1:
| 3 |
| 2 |
∴V小:V中:V大=23:33:43=8:27:64,
∴(V中-V小):(V大-V中)=(27-8):(64-27)=19:37,
即上、下两部分体积之比为19:37.
点评:本题考查求棱台被它的中截面分成的上、下两部分体积之比,考查学生的计算能力,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,在菱形ABCD中,对角线AC,BD交于E点,F,G分别为AD,BC的中点,AB=2,∠DAB=60°,沿对角线BD将△ABD折起,使得AC=
如图所示,在菱形ABCD中,对角线AC,BD交于E点,F,G分别为AD,BC的中点,AB=2,∠DAB=60°,沿对角线BD将△ABD折起,使得AC= 如图,A,B是双曲线
如图,A,B是双曲线 如图所示,已知正三棱柱ABC-A1B1C1的面对角线A1B⊥B1C,求证B1C⊥C1A.
如图所示,已知正三棱柱ABC-A1B1C1的面对角线A1B⊥B1C,求证B1C⊥C1A.