题目内容
 如图所示.△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,
如图所示.△ABC中,∠B=90°,M为AB上一点,使得AM=BC,N为BC上一点,使得CN=BM,连AN,CM交于P点.求∠APM的度数.
考点:相似三角形的性质
专题:立体几何
分析:可过A作AB的垂线,在其上截取AK=CN=MB,连KM,KC,得△KAM≌△MBC,进而由题中条件得出△KMC为等腰直角三角形,再证△AKC≌△CAN,得出∠KCA=∠NAC,即KC∥AN,进而可将∠APM转化为∠KCM求解.
解答:
解:如图,过A作AB的垂线,在其上截取AK=CN=MB,连KM,KC,则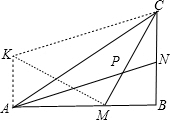
因为AM=BC,AK=BM,∠KAM=∠B=90°,
所以△KAM≌△MBC,
所以KM=CM,∠AMK=∠MCB
因为∠CMB+∠MCB=90°,
所以∠CMB+∠AMK=90°
所以∠KMC=90°
所以△KMC为等腰直角三角形,∠MCK=45°
又因为∠KAM=∠B=90°,AK=CN,
所以AK∥CN,
所以四边形ANCK是平行四边形,
所以KC∥AN,
所以∠APM=∠KCM=45°.

因为AM=BC,AK=BM,∠KAM=∠B=90°,
所以△KAM≌△MBC,
所以KM=CM,∠AMK=∠MCB
因为∠CMB+∠MCB=90°,
所以∠CMB+∠AMK=90°
所以∠KMC=90°
所以△KMC为等腰直角三角形,∠MCK=45°
又因为∠KAM=∠B=90°,AK=CN,
所以AK∥CN,
所以四边形ANCK是平行四边形,
所以KC∥AN,
所以∠APM=∠KCM=45°.
点评:本题主要考查了全等三角形的判定及性质以及等腰直角三角形的性质等问题,能够通过作辅助线在图形之间建立联系,进而辅助解题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
过直线y=-1上一点M向抛物线x2=4y作切线,切点分别为A、B,则直线AB恒过定点( )
| A、(0,1) |
| B、(0,2) |
| C、(1,1) |
| D、(-1,1) |
 如图,A,B是双曲线
如图,A,B是双曲线