题目内容
19.在等差数列{an}中,an>0,n=1,2,3,…,且其前n项和Sn满足4Sn=an2+2an-3.求:(1)a1的值;
(2)数列{an}的通项公式.
分析 (1)令n=1,列出方程解出a1;
(2)令n=2代入条件式子,计算a2,得出公差,写出通项公式.
解答 解:(1)∵4Sn=an2+2an-3,∴4a1=a12+2a1-3,解得a1=3或a1=-1.∵an>0,∴a1=3.
(2)当n=2时,4S2=a22+2a2-3,即4(3+a2)=a22+2a2-3,解得a2=5或a2=-3(舍).
∴等差数列{an}的公差d=a2-a1=2.
∴an=a1+(n-1)d=2n+1.
点评 本题考查了等差数列的通项公式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若sinα+cosα=-$\frac{7}{5}$,则角α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
7.下列命题中,正确的个数为( )
(1)函数y=$\frac{1}{{a}^{x}}$(a>0,a≠1)不是指数函数
(2)指数函数不具有奇偶性
(3)指数函数在其定义域上是单调函数.
(1)函数y=$\frac{1}{{a}^{x}}$(a>0,a≠1)不是指数函数
(2)指数函数不具有奇偶性
(3)指数函数在其定义域上是单调函数.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.如果平面α∥平面β,直线m?α,直线n?β,那么直线m,n的位置关系是( )
| A. | 平行 | B. | 异面 | C. | 平行或异面 | D. | 相交 |
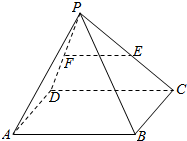 如图所示,P是平行四边形ABCD外一点,E,F分别是PC,PD的中点,判断EF与平面PAB是否平行?
如图所示,P是平行四边形ABCD外一点,E,F分别是PC,PD的中点,判断EF与平面PAB是否平行?