题目内容
14. 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点.(Ⅰ)证明:BD⊥面PAC
(Ⅱ)若G是PC的中点,求DG与APC所成的角的正弦值;
(Ⅲ)若G满足PC⊥面BGD,求二面角G-BD-A的余弦值.
分析 (Ⅰ)设AC∩BD=O,由△ABD≌△CBD,△ABO≌△CBO,得BD⊥AC,由线面垂直得PA⊥BD,由此能证明BD⊥面PAC;
(Ⅱ)由(Ⅰ)知BD⊥平面PAC,则∠DGO为直线DG与平面PAC所成的角,求解三角形可得DG与APC所成的角的正弦值;
(Ⅲ)由BD⊥平面PAC,可得OG⊥BD,OA⊥BD,得∠AOG为二面角G-BD-A的平面角,然后利用三角形相似求解.
解答 (Ⅰ)证明:设AC∩BD=O,∵AB=BC,AD=CD,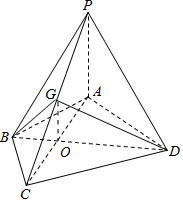
∴△ABD≌△CBD,得∠ABD=∠CBD,则△ABO≌△CBO,
∴∠AOB=∠COB=90°,故BD⊥AC,
∵PA⊥面ABCD,∴PA⊥BD,
∵PA∩AC=A,∴BD⊥面PAC;
(Ⅱ)解:由(Ⅰ)知BD⊥平面PAC,
故∠DGO为直线DG与平面PAC所成的角,
在Rt△ABC中,由AB=2,∠ABO=60°,得AO=$\sqrt{3}$,
在Rt△ADO中,由AD=$\sqrt{7}$,AO=$\sqrt{3}$,得DO=2,
又GO=$\frac{1}{2}$PA=$\frac{\sqrt{3}}{2}$,
∴DG=$\sqrt{O{D}^{2}+O{G}^{2}}=\frac{\sqrt{19}}{2}$,则sin∠DGO=$\frac{OD}{DG}=\frac{2}{\frac{\sqrt{19}}{2}}=\frac{4\sqrt{19}}{19}$.
∴DG与平面APC所成的角的正弦值为$\frac{4\sqrt{19}}{19}$;
(Ⅲ)解:由BD⊥平面PAC,可得OG⊥BD,OA⊥BD,
∴∠AOG为二面角G-BD-A的平面角,
∵PC⊥面BGD,∴PG⊥GO,则Rt△PAC∽Rt△OGC,
∴cos∠COG=cos∠CPA=$\frac{PA}{PC}$,
∵PA=$\sqrt{3}$,AC=2AO=$2\sqrt{3}$,
∴PC=$\sqrt{P{A}^{2}+A{C}^{2}}=\sqrt{15}$,
则cos∠COG=cos∠CPA=$\frac{PA}{PC}$=$\frac{\sqrt{3}}{\sqrt{15}}=\frac{\sqrt{5}}{5}$.
则cos∠AOG=-cos∠COG=$-\frac{\sqrt{5}}{5}$.
故二面角G-BD-A的余弦值为-$\frac{\sqrt{5}}{5}$.
点评 本题考查线面垂直的判定,考查线面角及面面角的求法,考查空间想象能力和思维能力,是中档题.

| 目的地/频数/运输时间 | 1 | 2 | 3 | 4 | 5 |
| 甲地 | 2 | 4 | 3 | 1 | |
| 乙地 | 1 | 3 | 4 | 2 |
(1)问运往甲地或乙地的新鲜荔枝每吨利润不低于80元的概率;
(2)设运到乙地的新鲜荔枝每吨利润为随机变量ξ,求ξ的分布列和数学期望Eξ;
(3)在同一批次中,把吨位数相同的新鲜荔枝运到甲地和运到乙地所获利润分别为X、Y,求事件“X>Y”发生的概率.
| A. | $g(x)=sin(4x+\frac{π}{6})$ | B. | $g(x)=sin(4x-\frac{π}{3})$ | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | g(x)=sin2x |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
| A. | 10万元 | B. | 11万元 | C. | 12万元 | D. | 13万元 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |