题目内容
19.已知数列{an}是以t为首项,以2为公差的等差数列,数列{bn}满足2bn=(n+1)an.若对n∈N*都有bn≥b4成立,则实数t的取值范围是[-18,-14].分析 依题意,可求得bn=$\frac{1}{2}$(n+1)an=(n+1)(2n+t-2),分离参数t,得到t(n-4)≥-2(n-4)(n+4),再对n-4=0,n-4<0,n-4>0分类讨论,即可求得实数t的取值范围.
解答 解:∵an=t+(n-1)×2=2n+t-2,
∴2bn=(n+1)an=(n+1)(2n+t-2),
∵对n∈N*都有bn≥b4成立,
即$\frac{1}{2}$(n+1)(2n+t-2)≥$\frac{1}{2}$(4+1)(2×4+t-2),
整理得:t(n-4)≥32-2n2=-2(n-4)(n+4),
若n=4,则0≥0,恒成立,故t∈R①;
若1≤n<4,则t≤-2(n+4)min=-2(3+4)=-14②;
若n>4,则t≥-2(n+4)max=-2(5+4)=-18③,
综合①②③,若对n∈N*都有bn≥b4成立,则-18≤t≤-14,
故答案为:[-18,-14].
点评 本题考查数列递推式,依题意,分离参数t,得到t(n-4)≥-2(n-4)(n+4)是关键,也是难点,考查等价转化思想与分类讨论思想的综合运用,考查逻辑思维能力与运算能力,属于难题.

练习册系列答案
相关题目
9.若等比数列{an}满足a2•a4=$\frac{1}{2}$,则a1a32a5=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
10.在锐角△ABC中,sinA=$\frac{2\sqrt{6}}{5}$,cosC=$\frac{5}{7}$,BC=7,若动点P满足$\overrightarrow{AP}$=$\frac{λ}{2}$$\overrightarrow{AB}$+(1-λ)$\overrightarrow{AC}$(λ∈R),则点P轨迹与直线AB,AC所围成的封闭区域的面积( )
| A. | 3$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 6$\sqrt{6}$ | D. | 12$\sqrt{6}$ |
4.设全集U是实数集R,集合M={x|x2>2x},N=$\left\{{x|\frac{2-x}{x-1}≥0}\right\}$,则(∁UM)∩N为( )
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1<x≤2} | D. | {x|1≤x<2} |
11.下列各组函数中,表示同一函数的是( )
| A. | y=1,y=$\frac{x}{x}$ | B. | y=$\frac{{x}^{2}-x}{x}$与y=x-1 | C. | y=x,y=$\root{3}{{x}^{3}}$ | D. | y=|x|,y=($\sqrt{x}$)2 |
8.$\sqrt{1-2sin(\frac{π}{2}+2)cos(\frac{π}{2}+2)}$的值是( )
| A. | sin2-cos2 | B. | cos2-sin2 | C. | -(sin2+cos2) | D. | sin2+cos2 |
9.已知a=2${\;}^{\frac{1}{3}}$,b=log3$\frac{2}{3}$,c=log${\;}_{\frac{1}{2}}$$\frac{1}{3}$,则( )
| A. | a>b>c | B. | a>c>b | C. | c>a>b | D. | c>b>a |
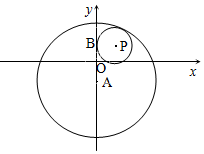 已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.
已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.