题目内容
17.若集合A={x|(k-1)x2+x-k=0}有且仅有两个子集,则实数k的值是1或$\frac{1}{2}$.分析 若A恰有两个子集,则A为单元素集,所以关于x的方程(a-1)x2-2x+1=0恰有一个实数解,分类讨论能求出实数k的取值.
解答 解:由题意可得集合A为单元素集
(1)当k=1时 A={x|x-1=0}={1};
(2)当k≠1时 则△=1+4k(k-1)=0解得k=$\frac{1}{2}$;
综上所述,实数 a的值是1或$\frac{1}{2}$.
故答案是:1或$\frac{1}{2}$.
点评 本题考查根据子集与真子集的概念,实数k的取值范围的求法,解题时要认真审题,注意分析法、讨论法和等价转化法的合理运用.

练习册系列答案
相关题目
5.按照如图的程序框图执行,若输出结果为31,则M处条件可以是( )


| A. | k>32 | B. | k≥16 | C. | k≥32 | D. | k<16 |
2.已知集合M={-1,0,1,2},N={y|y=2x+1,x∈M},则M∩N=( )
| A. | {-1,1} | B. | {1,2} | C. | {-1,1,3,5} | D. | {-1,0,1,2} |
9.若等比数列{an}满足a2•a4=$\frac{1}{2}$,则a1a32a5=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
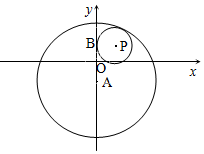 已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.
已知圆A:x2+(y+3)2=100,圆A内一定点B(0,3),圆P过B且与圆A内切,如图所示,求圆心P的轨迹方程.